题目内容
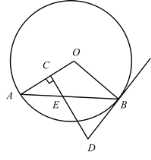
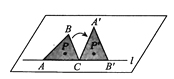
【题目】如图,在平整的桌面上面一条直线l,将三边都不相等的三角形纸片ABC平放在桌面上,使AC与边l对齐,此时△ABC的内心是点P;将纸片绕点C顺时针旋转,使点B落在l上的点B'处,点A落在A'处,得到△A'B'C'的内心点P'.下列结论正确的是( )
A.PP'与l平行,PC与P'B'平行
B.PP'与l平行,PC与P'B'不平行
C.PP'与l不平行,PC与P'B'平行
D.PP'与l不平行,PC与P'B'不平行
【答案】B
【解析】
如图,连接CP、CP′、PP′、P′B′,根据旋转可得三角形PP′C是等腰三角形,可得2∠CPP′+∠PCP′=180°,再根据△ABC的内心是点P,可得2∠ACP+∠PCP′=180°,从而∠CPP′=∠ACP,可以判断PP′∥![]() ;根据∠BCA≠∠A′B′C,可得∠PCA≠∠P′B′C,即可判断PC与P′B′不平行,即可得结论.
;根据∠BCA≠∠A′B′C,可得∠PCA≠∠P′B′C,即可判断PC与P′B′不平行,即可得结论.
如图,连接CP、CP′、PP′、P′B′,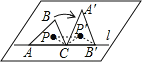
∵三角形纸片ABC绕点C顺时针旋转,
∴CP=CP′,
∴∠CPP′=∠CP′P,
∴2∠CPP′+∠PCP′=180°,
∵△ABC的内心是点P,
∴∠ACP=![]() ∠ACB,
∠ACB,
∵∠A′CB′=∠ACB,∠B′CP′=![]() ∠A′CB′,
∠A′CB′,
∴2∠ACP+∠PCP′=180°,
∴∠CPP′=∠ACP,
∴PP′∥![]() ;
;
∵∠BCA≠∠A′B′C,
∴∠PCA≠∠P′B′C,
∴PC与P′B′不平行.
所以PP′与![]() 平行,PC与P′B′不平行.
平行,PC与P′B′不平行.
故选:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目