题目内容
【题目】如图,在三角形ABC中, D , E , F三点分别在AB , AC , BC上,过点D的直线与线段EF的交点为点M , 已知2∠1-∠2=150°,2∠ 2-∠1=30°.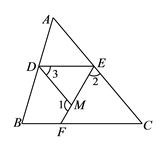
(1)求证:DM∥AC;
(2)若DE∥BC , ∠C =50°,求∠3的度数.
【答案】
(1)
证明:∵ 2∠1-∠2=150°,2∠2-∠1=30°,
∴ ∠1+∠2=180°.
∵ ∠1+∠DME=180°,
∴ ∠2=∠DME .
∴ DM∥AC .
(2)
解:∵ DM∥AC,
∴ ∠3=∠AED .
∵ DE∥BC ,
∴ ∠AED=∠C .
∴ ∠3=∠C .
∵ ∠C=50°,
∴ ∠3=50°.
【解析】(1) 已知 2∠1-∠2=150°,2∠2-∠1=30°,可得∠1+∠2=180°,再由∠1+∠DME=180°,可得∠2=∠DME , 根据内错角相等,两直线平行即可得DM∥AC;
(2) 由(1)得DM∥AC , 根据两直线平行,内错角相等可得∠3=∠AED ,再由DE∥BC ,可得∠AED=∠C ,所以∠3=∠C= 50°.
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.

练习册系列答案
相关题目
【题目】某商场服装部为了调动营业员的积极性,决定实行目标管理.为了确定一个适当的月销售日标,服装部统计了每位营业员在某月的销售额(单位:万元),数据如下:
销售额/万元 | 14 | 15 | 17 | 19 | 27 | 30 |
人数 | 1 | 6 | 3 | 4 | 5 | 1 |
(1)分别求出所有营业员月销售额的众数、中位数和平均数;
(2)如果想让一半左右的营业员有信心达到销售目标.月销售目标定为多少合适?