Question

【题目】如图，正方形ABCD的对角线相交于点O，∠CAB的平分线分别交BD、BC于E、F，作BH⊥AF于点H，分别交AC、CD于点G、P，连结GE、GF．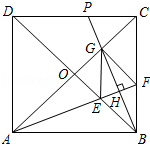
（1）求证：△OAE≌△OBG．
（2）试问：四边形BFGE是否为菱形？若是，请证明；若不是，请说明理由．

Answer 1

【答案】
（1）证明：∵四边形ABCD是正方形，

∴OA=OB，∠AOE=∠BOG=90°．

∵BH⊥AF，

∴∠AHG=∠AHB=90°，

∴∠GAH+∠AGH=90°=∠OBG+∠AGH，

∴∠GAH=∠OBG，

即∠OAE=∠OBG．

∴在△OAE与△OBG中， ，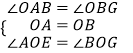

∴△OAE≌△OBG（ASA）；

（2）解：四边形BFGE为菱形；理由如下：

在△AHG与△AHB中， ，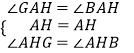

∴△AHG≌△AHB（ASA），

∴GH=BH，

∴AF是线段BG的垂直平分线，

∴EG=EB，FG=FB．

∵∠BEF=∠BAE+∠ABE=67.5°，∠BFE=90°﹣∠BAF=67.5°，

∴∠BEF=∠BFE，

∴EB=FB，

∴EG=EB=FB=FG，

∴四边形BFGE是菱形；

【解析】（1）由正方形的性质得出OA=OB，∠AOE=∠BOG=90°，再由角的互余关系证出∠OAE=∠OBG，由ASA即可证明△OAE≌△OBG；（2）先证明△AHG≌△AHB，得出GH=BH，由线段垂直平分线的性质得出EG=EB，FG=FB；再证出∠BEF=∠BFE，得出EB=FB，因此EG=EB=FB=FG，即可得出结论．