题目内容
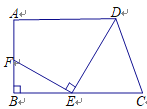
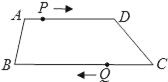
【题目】已知：如图，在梯形ABCD中，AD∥BC，AD＝24cm，BC＝30cm，点P自点A向D以1cm/s的速度运动，到D点即停止．点Q自点C向B以2cm/s的速度运动，到B点即停止，直线PQ截梯形为两个四边形．问当P，Q同时出发，几秒时其中一个四边形为平行四边形？
【答案】当8秒或10秒时，其中一个四边形是平行四边形.
【解析】试题分析：若四边形PDCQ或四边形APQB是平行四边形，那么QD=CQ或AP=BQ或PD=BQ，根据这个结论列出方程就可以求出时间．
试题解析：设P，Q同时出发t秒后四边形PDCQ或四边形APQB是平行四边形，根据已知得到AP=t，PD=24t，CQ=2t，BQ=302t.
(1)若四边形PDCQ是平行四边形，则PD=CQ，
∴24t=2t，
∴t=8，
∴8秒后四边形PDCQ是平行四边形；
(2)若四边形APQB是平行四边形，则AP=BQ，
∴t=302t，
∴t=10，
∴10秒后四边形APQB是平行四边形.
∴出发后8秒或10秒其中一个是平行四边形.
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与
，所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, 
，2, 
，2
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+（____） |
5×5 | （________） |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.
