题目内容
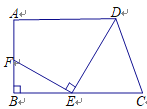
【题目】如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连接DE,作EF⊥DE,交直线AB于点F.
(1)若点F与B重合,求CE的长;(3分)
(2)若点F在线段AB上,且AF=CE,求CE的长.(5分)
【答案】(1)3;(2)5.
【解析】试题分析:(1)根据题意画出图形,得出矩形ABEC求出BE,即可求出CE;
(2)过D作DM⊥BC于M,得出四边形ABMD是矩形,推出AD=BM=9,AB=DM=7,CM=12-9=3,设AF=CE=a,则BF=7-a,EM=a-3,BE=12-a,求出∠BFE=∠DEM,∠B=∠DME,证△FBE∽△EMD,得出比例式![]() ,求出a即可.
,求出a即可.
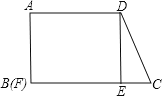
试题解析:(1)当F和B重合时,如图,
∵EF⊥DE,
∵DE⊥BC,
∵∠B=90°,
∴AB⊥BC,
∴AB∥DE,
∵AD∥BC,
∴四边形ABED是平行四边形,
∴AD=EF=9,
∴CE=BC-EF=12-9=3;
(2)过D作DM⊥BC于M,

∵∠B=90°,
∴AB⊥BC,
∴DM∥AB,
∵AD∥BC,
∴四边形ABMD是矩形,
∴AD=BM=9,AB=DM=7,CM=12-9=3,
设AF=CE=a,则BF=7-a,EM=a-3,BE=12-a,
∵∠FEC=∠B=∠DMB=90°,
∴∠FEB+∠DEM=90°,∠BFE+∠FEB=90°,
∴∠BFE=∠DEM,
∵∠B=∠DME,
∴△FBE∽△EMD,
∴![]() ,
,
∴![]() ,
,
a=5,a=17,
∵点F在线段AB上,AB=7,
∴AF=CE=17(舍去),
即CE=5.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目