Question

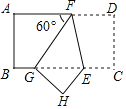
【题目】如图，在矩形ABCD中，点F在AD上，点E在BC上，把这个矩形沿EF折叠后，使点D恰好落在BC边上的G点处，若矩形面积为且，GE=2BG，则折痕EF的长为（ ）

A. 4 B. C. 2 D.

Answer 1

【答案】D

【解析】

由折叠的性质可知，DF=GF、HE=CE、GH=DC、∠DFE=∠GFE，结合∠AFG=60°即可得出∠GFE=60°，进而可得出△GEF为等边三角形．在Rt△GHE中，通过解含30度角的直角三角形及勾股定理即可得出GE=2EC、DC=EC，再由GE=2BG结合矩形面积为8，即可求出EC的长度，根据EF=GE=2EC即可求出结论．

由折叠的性质可知，DF=GF，HE=CE，GH=DC，∠DFE=∠GFE．

∵∠GFE+∠DFE=180°﹣∠AFG=120°，∴∠GFE=60°．

∵AF∥GE，∠AFG=60°，∴∠FGE=∠AFG=60°，∴△GEF为等边三角形，∴EF=GE．

∵∠FGE=60°，∠FGE+∠HGE=90°，∴∠HGE=30°．

在Rt△GHE中，∠HGE=30°，∴GE=2HE=2CE，∴GH==HE=CE．

∵GE=2BG，∴BC=BG+GE+EC=4EC．

∵矩形ABCD的面积为8，∴4ECEC=8，∴EC=，EF=GE=2．

故选D．