题目内容
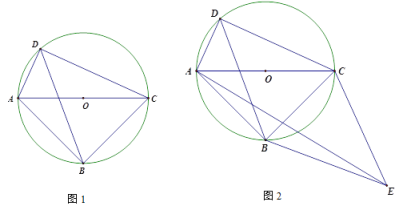
【题目】如图1,⊙O是△ABC的外接圆,点D是![]() 上一动点(不与点A、C重合),且∠ADB=∠BAC=45°.
上一动点(不与点A、C重合),且∠ADB=∠BAC=45°.
(1)求证:AC是⊙O的直径;
(2)当点D在![]() 运动到使AD+CD=5
运动到使AD+CD=5![]() 时,则线段BD的长为 ;(直接写出结果)
时,则线段BD的长为 ;(直接写出结果)
(3)如图2,把△DBC沿直线BC翻折得到△EBC,连接AE,当点D在![]() 运动时,探究线段AE、BD、CD之间的数量关系,并说明理由.
运动时,探究线段AE、BD、CD之间的数量关系,并说明理由.
【答案】(1)见解析;(2)5;(3)AE2=2BD2+CD2,理由见解析.
【解析】
(1)根据圆周角定理,可得∠BDC=∠BAC=45°,可求出∠ADC=90°根据圆周角定理的推论可得结论;
(2)作AM⊥BD于M,CN⊥BD于N,由等腰直角三角形的性质得AD=![]() DM,CE=
DM,CE=![]() DN,证△ABM≌△BCN,可得BN=AM=DM,即可得出BD=BN+DN,从而求得BD的长;
DN,证△ABM≌△BCN,可得BN=AM=DM,即可得出BD=BN+DN,从而求得BD的长;
(3)延长DA到点F,使得AF=CD,连接BF,由(2)得BD=![]() (AD+CD)=
(AD+CD)=![]() DF,可得△BDF为等腰直角三角形,则BF=BD,DF2=2BD2,连接CF,证△CBF≌△ABE,可得AE=CF,在Rt△FDC中,CF2=DF2+CD2,即AE2=2BD2+CD2.
DF,可得△BDF为等腰直角三角形,则BF=BD,DF2=2BD2,连接CF,证△CBF≌△ABE,可得AE=CF,在Rt△FDC中,CF2=DF2+CD2,即AE2=2BD2+CD2.
(1)证明:∵∠BDC、∠BAC都是![]() 所对的圆周角,∠BAC=45°
所对的圆周角,∠BAC=45°
∴∠BDC=∠BAC=45°
∵∠ADB=45°
∴∠ADC=∠ADB+∠BDC=90°
∴AC是⊙O的直径;
(2)作AM⊥BD于M,CN⊥BD于N
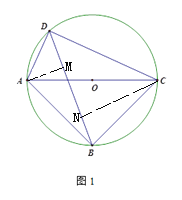
∵∠BDC=∠ADB =45°
∴△ADM,△CDN为等腰直角三角形
∴DM=AM=![]() AD, DN=CN=
AD, DN=CN=![]() CD
CD
∵AC是直径,∠BAC=45°
∴△ABC为等腰直角三角形
∴∠ABC =∠ABM+∠NBC=90°,AB=BC
∵AM⊥BD,CN⊥BD
∴∠AMB=∠BNC=∠BCN+∠NBC =90°
∴∠ABM=∠BCN
△ABM≌△BCN
∴BN=AM=DM=![]() AD
AD
∵AD+CD=5![]()
∴BD=BN+DN=![]() AD+
AD+![]() CD=
CD=![]() ×5
×5![]() =5;
=5;
(3)延长DA到点F,使得AF=CD,连接BF
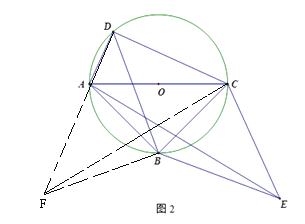
由(2)得BD=![]() (AD+CD)=
(AD+CD)=![]() DF,
DF,
∵∠ADB =45°
∴△BDF为等腰直角三角形
∴BF=BD,DF2=2BD2
连接CF,
在△AFB和△CDB中
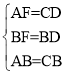
∴△AFB≌△CDB
∴∠ABF=∠CBD
又∵把△DBC沿直线BC翻折得到△EBC
∴∠CBE=∠CBD,BD=BE
∴∠ABF+∠ABC=∠CBE+∠ABC,即∠CBF=∠ABE,BF=BE
∵AB=CB
∴△CBF≌△ABE
∴AE=CF
∴在Rt△FDC中,CF2=DF2+CD2
即AE2=2BD2+CD2.

 阅读快车系列答案
阅读快车系列答案【题目】射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为![]() ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.