题目内容
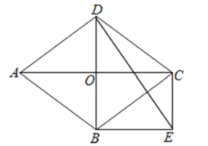
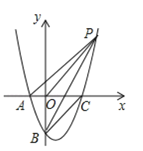
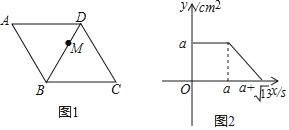
【题目】如图,已知平行四边形ABCD中,AB=BC,点M从点D出发,沿D→C→A以1cm/s的速度匀速运动到点A,图2是点M运动时,△MAB的面积y(cm2)随时间x(s)变化的关系图象,则边AB的长为( )cm.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
先由图2分析计算出DC,AB,BC,AC的长,及三角形MAB的面积;易判定平行四边形ABCD为菱形,从而其对角线垂直,从而连接对角线,得直角三角形,利用勾股定理建立方程,从而求得a值,进而得AB的长.
解:由图2可知,点M从点D到点C时,△MAB的面积一直为a,
∴DC=a,AB=BC=a,S△MAB=a,
当点M从点C运动到点A时,S△MAB逐渐减小,直到为0,
![]()
连接BD,交AC于点O,
∵AB=BC,
∴平行四边形ABCD为菱形,
∴AC⊥BD,
![]()
∵S△MAB=a,
![]()
解得![]()
∴边AB的长为![]() cm.
cm.
故选A.

练习册系列答案
相关题目
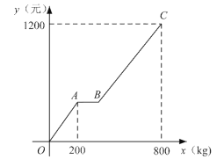
【题目】某商店代理销售一种水果,六月份的销售利润![]() (元)与销售量
(元)与销售量![]() 之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
之间函数关系的图像如图中折线所示.请你根据图像及这种水果的相关销售记录提供的信息,解答下列问题:
日期 | 销售记录 |
6月1日 | 库存 |
6月9日 | 从6月1日至今,一共售出 |
6月10、11日 | 这两天以成本价促销,之后售价恢复到10元/ |
6月12日 | 补充进货 |
6月30日 |
|
(1)截止到6月9日,该商店销售这种水果一共获利多少元?
(2)求图像中线段![]() 所在直线对应的函数表达式.
所在直线对应的函数表达式.