��Ŀ����
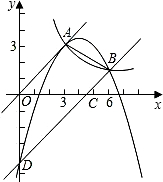
��ͼ����֪�����������ͷ�����������ͼ������A��3��3������1���������������ͷ����������Ľ���ʽ��
��2����ֱ��OA����ƽ�ƺ��뷴����������ͼ���ڵ�B��6��m������m��ֵ�����һ�κ����Ľ���ʽ��
��3���ڣ�2�����е�һ�κ�����ͼ����x�ᡢy��ֱ���C��D�����A��B��D����Ķ��κ����Ľ���ʽ��
��4���ڵڣ�3���ʵ������£����κ����ڵ�һ����ͼ�����Ƿ���ڵ�E��ʹ�ı���OECD�����S1����
 ����OABD�����S���㣺S1=
����OABD�����S���㣺S1=| 2 | 3 |
��������1����������������ͷ����������Ľ���ʽ���ô���ϵ�������
��2����ΪB��Ϊ���������Ľ��㣬��B��6��m��������֪����y=
���������m��ֵ������һ�κ���������������ƽ�У���֪���߱���ϵ����ͬ�����ô���ϵ�������b��ֵ��
��3��A��B�����������D������ɸ���һ�κ�������ʽ��ã�
��4������ͼ�Σ�������֪�������꣬�����Ӧ�߶γ��������ı��β����ʽ������ת��Ϊ�������������������IJ������������ĺͣ�
��2����ΪB��Ϊ���������Ľ��㣬��B��6��m��������֪����y=
| 9 |
| x |
��3��A��B�����������D������ɸ���һ�κ�������ʽ��ã�
��4������ͼ�Σ�������֪�������꣬�����Ӧ�߶γ��������ı��β����ʽ������ת��Ϊ�������������������IJ������������ĺͣ�
����⣺��1���������������Ľ���ʽΪy=k1x��k1��0����
��Ϊy=k1x��ͼ�����A��3��3����
����3=3k1�����k1=1��
��������������Ľ���ʽΪy=x��
�跴���������Ľ���ʽΪy=
��k2��0����
��Ϊy=
��ͼ�����A��3��3����
����3=
��
���k2=9��
��������������Ľ���ʽΪy=
����2�֣�
��2������B��6��m����y=
��ͼ���ϣ�
����m=
=
��
���B��6��
������3�֣�
��һ�κ�������ʽΪy=k3x+b��k3��0����
��Ϊy=k3x+b��ͼ������y=xƽ�Ƶõ��ģ�
����k3=1����y=x+b��
����Ϊy=x+b��ͼ�����B��6��
����
����
=6+b��
���b=-
��
��һ�κ����Ľ���ʽΪy=x-
��
��3����Ϊy=x-
��ͼ��y���ڵ�D��
����D��������0��-
����
����κ����Ľ���ʽΪy=ax2+bx+c��a��0����
��Ϊy=ax2+bx+c��ͼ�����A��3��3����B��6��
������D��0��-
����
����
��
���
��
������κ����Ľ���ʽΪy=-
x2+4x-
����6�֣�
��4����y=x-
��x���ڵ�C��
���C�������ǣ�
��0����
��ͼ��ʾ������OE��CE������A��AF��x�ᣬ��y���ڵ�F������B��BH��y�ᣬ��AF�ڵ�H������D��DG��x�ᣬ��ֱ��BH�ڵ�G����S=
��6-
��6��6-
��
��3-
��3��3=45-18-
-
=
��
������ڵ�E��x0��y0����ʹS1=
S=
��
=
��
���ı���CDOE�Ķ���Eֻ����x���Ϸ���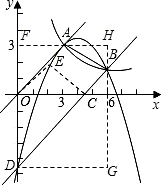
��y0��0��
��S1=S��OCD+S��OCE=
��
��
+
��
•y0=
+
y0��
��
+
y0=
��
��y0=
����7�֣�
��E��x0��y0���ڶ��κ�����ͼ���ϣ�
��-
+4x0-
=
��
���x0=2��x0=6��
��x0=6ʱ����E��6��
�����B�غϣ���ʱCDOE�����ı��Σ���x0=6��ȥ��
���E��������2��
������8�֣�
��Ϊy=k1x��ͼ�����A��3��3����
����3=3k1�����k1=1��
��������������Ľ���ʽΪy=x��
�跴���������Ľ���ʽΪy=
| k2 |
| x |
��Ϊy=
| k2 |
| x |
����3=
| k2 |
| 3 |
���k2=9��
��������������Ľ���ʽΪy=
| 9 |
| x |
��2������B��6��m����y=
| 9 |
| x |
����m=
| 9 |
| 6 |
| 3 |
| 2 |
���B��6��
| 3 |
| 2 |
��һ�κ�������ʽΪy=k3x+b��k3��0����
��Ϊy=k3x+b��ͼ������y=xƽ�Ƶõ��ģ�
����k3=1����y=x+b��
����Ϊy=x+b��ͼ�����B��6��
| 3 |
| 2 |
����
| 3 |
| 2 |
���b=-
| 9 |
| 2 |
��һ�κ����Ľ���ʽΪy=x-
| 9 |
| 2 |
��3����Ϊy=x-
| 9 |
| 2 |
����D��������0��-
| 9 |
| 2 |
����κ����Ľ���ʽΪy=ax2+bx+c��a��0����
��Ϊy=ax2+bx+c��ͼ�����A��3��3����B��6��
| 3 |
| 2 |
| 9 |
| 2 |
����
|
���
|
������κ����Ľ���ʽΪy=-
| 1 |
| 2 |
| 9 |
| 2 |
��4����y=x-
| 9 |
| 2 |
���C�������ǣ�
| 9 |
| 2 |
��ͼ��ʾ������OE��CE������A��AF��x�ᣬ��y���ڵ�F������B��BH��y�ᣬ��AF�ڵ�H������D��DG��x�ᣬ��ֱ��BH�ڵ�G����S=
| 15 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 9 |
| 2 |
| 81 |
| 4 |
������ڵ�E��x0��y0����ʹS1=
| 2 |
| 3 |
| 81 |
| 4 |
| 2 |
| 3 |
| 27 |
| 2 |
���ı���CDOE�Ķ���Eֻ����x���Ϸ���

��y0��0��
��S1=S��OCD+S��OCE=
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 81 |
| 8 |
| 9 |
| 4 |
��
| 81 |
| 8 |
| 9 |
| 4 |
| 27 |
| 2 |
��y0=
| 3 |
| 2 |
��E��x0��y0���ڶ��κ�����ͼ���ϣ�
��-
| 1 |
| 2 |
| x | 2 0 |
| 9 |
| 2 |
| 3 |
| 2 |
���x0=2��x0=6��
��x0=6ʱ����E��6��
| 3 |
| 2 |
���E��������2��
| 3 |
| 2 |
���������⽫������ѧ������Ҫ������һ�κ������������������������������������κ�������������������ô���ϵ������������ʽ������������Ĺ�ϵ��������ͼ����������ۺ��Խ�ǿ���Ѷ����У�

��ϰ��ϵ�д�
�����Ŀ
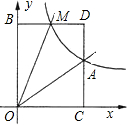 ��ͼ����֪����������y=ax�뷴��������y=
��ͼ����֪����������y=ax�뷴��������y=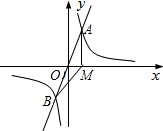 ��Ϊ1������A��x��Ĵ��ߣ�����ΪM������BM��
��Ϊ1������A��x��Ĵ��ߣ�����ΪM������BM�� ��ͼ����֪����������y=kx��ͼ����A��-
��ͼ����֪����������y=kx��ͼ����A��- ��ͼ����֪�����������ͷ�����������ͼ������A��3��3����
��ͼ����֪�����������ͷ�����������ͼ������A��3��3����