题目内容
 如图,已知正比例函数y=kx的图象经过点A(-2
如图,已知正比例函数y=kx的图象经过点A(-2| 3 |
| 3 |
(1)求k和a的值;
(2)若一次函数y=nx+2的图象经过点A,并且与X轴相交于点M,问:在x轴上是否存在点P,使得以三点P、A、M组成的三角形AMP为等腰三角形?如果存在,请求出点P的坐标;如果不存在,请说明理由.
分析:(1)根据坐标可以得到:OB=2
,AB=a,根据△A0B的面积为4
,即可求得a的值,把A的坐标代入解析式即可求得k的值;
(2)把A坐标代入一次函数解析式求得n的值,就可求出M的坐标,根据等腰三角形的性质即可求得P的坐标.
| 3 |
| 3 |
(2)把A坐标代入一次函数解析式求得n的值,就可求出M的坐标,根据等腰三角形的性质即可求得P的坐标.
解答:解:(1)∵OB=2
,AB=a
OB•AB=4
.
即:
•2
•a=4
解得:a=4
把A的坐标代入正比例函数解析式得到k=-
.
(2)把A(-2
,4)代入y=nx+2,
得到:-2
n+2=4,解得:n=-
.
即直线的解析式是:y=-
x+2.令y=0,解得:x=2
.即M的坐标是(2
,0).
AM=
=8.
当PM=AM时,P点的坐标是(8+2
,0)或(2
-8,0);
当AP=AM时,P与M关于AB对称,则P的坐标是(-6
,0);
当AP=MP时,P是线段AM的中垂线与x轴的交点,则P的坐标是(2
-
,0).
| 3 |
| 1 |
| 2 |
| 3 |
即:
| 1 |
| 2 |
| 3 |
| 3 |
解得:a=4
把A的坐标代入正比例函数解析式得到k=-
2
| ||
| 3 |
(2)把A(-2
| 3 |
得到:-2
| 3 |
| ||
| 3 |
即直线的解析式是:y=-
| ||
| 3 |
| 3 |
| 3 |
AM=
(4
|
当PM=AM时,P点的坐标是(8+2
| 3 |
| 3 |
当AP=AM时,P与M关于AB对称,则P的坐标是(-6
| 3 |
当AP=MP时,P是线段AM的中垂线与x轴的交点,则P的坐标是(2
| 3 |
8
| ||
| 3 |
点评:注意已知三角形是等腰三角形时,要注意进行讨论.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 边形OABD的面积S满足:S1=
边形OABD的面积S满足:S1=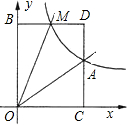 如图,已知正比例函数y=ax与反比例函数y=
如图,已知正比例函数y=ax与反比例函数y=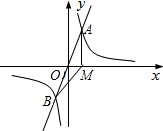 标为1,过点A作x轴的垂线,垂足为M,连接BM.
标为1,过点A作x轴的垂线,垂足为M,连接BM. 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).