题目内容
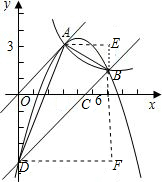
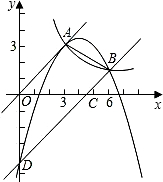
 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).(1)求正比例函数和反比例函数的解析式;
(2)把直线OA向下平移后与反比例函数的图象交于点B(6,m),求m的值和这个一次函数的解析式;
(3)第(2)问中的一次函数的图象与x轴、y轴分别交于C、D,求过A、B、D三点的三角形的面积.
分析:(1)利用待定系数法,由正比例函数和反比例函数的图象都经过点A(3,3),即可求得解析式;
(2)由点B在反比例函数图象上,即可求得m的值;又由此一次函数是正比例函数平移得到的,可知一次函数与反比例函数的比例系数相同,代入点B的坐标即可求得解析式;
(3)构造直角梯形AEFD,则通过求解△ABE、△BDF与直角梯形ADFE的面积即可求得△ABD的面积.
(2)由点B在反比例函数图象上,即可求得m的值;又由此一次函数是正比例函数平移得到的,可知一次函数与反比例函数的比例系数相同,代入点B的坐标即可求得解析式;
(3)构造直角梯形AEFD,则通过求解△ABE、△BDF与直角梯形ADFE的面积即可求得△ABD的面积.
解答:解:(1)设正比例函数的解析式为y=ax,反比例函数的解析式为y=
,
∵正比例函数和反比例函数的图象都经过点A(3,3),
∴3=3a,3=
,
∴a=1,b=9,
∴正比例函数的解析式为y=x,反比例函数的解析式为y=
;
(2)∵点B在反比例函数上,
∴m=
=
,
∴B点的坐标为(6,
),
∵直线BD是直线OA平移后所得的直线,
∴可设直线BD的解析式为y=x+b,
∴
=6+b,
∴b=-
,
∴这个一次函数的解析式为y=x-
;
(3)过点B作EF∥y轴,过点A作AE∥x轴交EF于E,过点D作DF∥x轴交EF于F,
∴点E的坐标为(6,3),点F的坐标为(6,-
),
∵点D在直线BD上,
∴点D的坐标为(0,-
),
∴AE=3,EF=3+
=
,DF=6,BE=3-
=
,BF=
+
=6,
∴S△ABD=S梯形AEFD-S△ABE-S△BDF
=
(AE+DF)•EF-
AE•BE-
DF•EF
=
×(3+6)×
-
×3×
-
×6×6=
.
| b |
| x |
∵正比例函数和反比例函数的图象都经过点A(3,3),
∴3=3a,3=
| b |
| 3 |
∴a=1,b=9,
∴正比例函数的解析式为y=x,反比例函数的解析式为y=
| 9 |
| x |
(2)∵点B在反比例函数上,
∴m=
| 9 |
| 6 |
| 3 |
| 2 |

∴B点的坐标为(6,
| 3 |
| 2 |
∵直线BD是直线OA平移后所得的直线,
∴可设直线BD的解析式为y=x+b,
∴
| 3 |
| 2 |
∴b=-
| 9 |
| 2 |
∴这个一次函数的解析式为y=x-
| 9 |
| 2 |
(3)过点B作EF∥y轴,过点A作AE∥x轴交EF于E,过点D作DF∥x轴交EF于F,
∴点E的坐标为(6,3),点F的坐标为(6,-
| 9 |
| 2 |
∵点D在直线BD上,
∴点D的坐标为(0,-
| 9 |
| 2 |
∴AE=3,EF=3+
| 9 |
| 2 |
| 15 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
∴S△ABD=S梯形AEFD-S△ABE-S△BDF
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 15 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 27 |
| 2 |
点评:此题考查了待定系数法求函数的解析式与三角形面积的求解方法等知识.主要考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
 边形OABD的面积S满足:S1=
边形OABD的面积S满足:S1=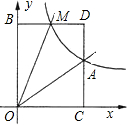 如图,已知正比例函数y=ax与反比例函数y=
如图,已知正比例函数y=ax与反比例函数y=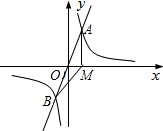 标为1,过点A作x轴的垂线,垂足为M,连接BM.
标为1,过点A作x轴的垂线,垂足为M,连接BM. 如图,已知正比例函数y=kx的图象经过点A(-
如图,已知正比例函数y=kx的图象经过点A(-