题目内容
【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF。
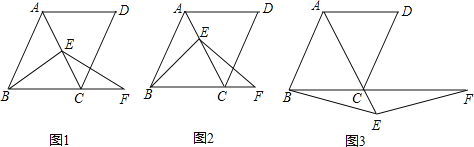
(1)若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(2)若E是线段AC或AC延长线上的任意一点,其它条件不变, 如图2、图3,线段BE、EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明。
【答案】(2)BE=EF,证明见解析
【解析】解:(2)图2:BE=EF。图3。
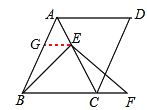
图2证明如下:过点E作EG∥BC,交AB于点G,
∵四边形ABCD为菱形,∴AB=BC。
又∵∠ABC=60°,∴△ABC是等边三角形。
∴AB=AC,∠ACB=60°。
又∵EG∥BC,∴∠AGE=∠ABC=60°。
又∵∠BAC=60°,∴△AGE是等边三角形。∴AG=AE。∴BG=CE。
又∵CF=AE,∴GE=CF。
又∵∠BGE=∠ECF=120°,∴△BGE≌△ECF(SAS)。∴BE=EF。
(1)根据菱形的性质结合∠ABC=60°可得△ABC是等边三角形,再根据等腰三角形三线合一的性质可得∠CBE=![]() ∠ABC=30°,AE=CE,所以CE=CF,然后等边对等角的性质可得∠F=∠CEF,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠F=30°,从而得到∠CBE=∠F,根据等角对等边的性质即可证明。
∠ABC=30°,AE=CE,所以CE=CF,然后等边对等角的性质可得∠F=∠CEF,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠F=30°,从而得到∠CBE=∠F,根据等角对等边的性质即可证明。
(2)图2,过点E作EG∥BC,交AB于点G,

根据菱形的性质结合∠ABC=60°可得△ABC是等边三角形,根据等边三角形的性质得到AB=AC,∠ACB=60°,再求出△AGE是等边三角形,根据等边三角形的性质得到AG=AE,从而可以求出BG=CE,再根据等角的补角相等求出∠BGE=∠ECF=120°,然后利用“边角边”证明△BGE和△ECF 全等,根据全等三角形对应边相等即可得证。
图3,证明思路与方法与图2完全相同, 证明如下:
过点E作EG∥BC交AB延长线于点G,
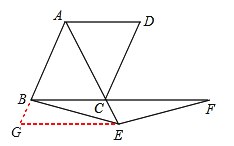
∵四边形ABCD为菱形,∴AB=BC。
又∵∠ABC=60°,∴△ABC是等边三角形。
∴AB=AC∠ACB=60°。
又∵EG∥BC,∴∠AGE=∠ABC=60°。
又∵∠BAC=60°,∴△AGE是等边三角形。∴AG=AE。∴BG=CE。
又∵CF=AE,∴GE=CF。
又∵∠BGE=∠ECF=60°,∴△BGE≌△ECF(SAS)。∴BE=EF。