题目内容
【题目】如图，AB∥CD，直线EF与AB、CD分别相交于E、F两点，EP平分∠AEF，过点F作FP⊥EP，若∠PEF=30°，则∠PFC等于（ ）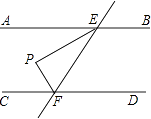
A.30°
B.45°
C.60°
D.120°
【答案】C
【解析】解：∵EP平分∠AEF，∠PEF=30°，
∴∠AEF=2∠PEF=60°，
∵AB∥CD，
∴∠CFE=180°﹣∠AEF=120°，
∵FP⊥EP，
∴∠P=90°，
∵∠PEF=30°，
∴∠PFE=60°，
∴∠PFC=∠CFE﹣∠PFE=120°﹣60°=60°．
所以答案是：C．
【考点精析】掌握垂线的性质和平行线的性质是解答本题的根本，需要知道垂线的性质：1、过一点有且只有一条直线与己知直线垂直．2、垂线段最短；两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．
练习册系列答案
相关题目
