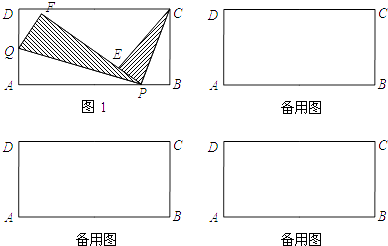
��Ŀ����
����Ŀ����ͼ����֪������y=��x2+bx+9��b2��bΪ��������������ԭ��O������x�ύ����һ��E���䶥��M�ڵ�һ���ޣ�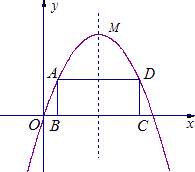
��1���������������Ӧ�ĺ�����ϵʽ��
��2�����A�Ǹ���������λ��x���Ϸ���������Գ�������һ�����㣻����A��x���ƽ���߽�������������һ��D������AB��x���ڵ�B��DC��x���ڵ�C��
�ٵ��߶�AB��BC�ij�������������λ����ʱ�������ABCD���ܳ���
�������ABCD���ܳ������ֵ����д����ʱ��A�����ꣻ
�۵�����ABCD���ܳ�ȡ�����ֵʱ����������Ƿ�Ҳͬʱȡ�����ֵ�����жϲ�˵�����ɣ�
���𰸡�
��1��
�⣺�����⣬����ԭ�㵽���κ�������ʽ
��9��b2=0��
���b=��3��
�����������ߵĶԳ������0��
![]() ��
��
����b=3��
���Խ���ʽΪy=��x2+3x
��2��
�⣺��A�������Ϊm���� ![]() ��m��0��
��m��0��
AB=3m��m2��BC=2�� ![]() ��m��=3��2m��
��m��=3��2m��
�����ABCD���ܳ�=2��AB+BC��=2����m2+m+3��=��2m2+2m+6��
�ٵ��߶�AB��BC�ij�������������λ����ʱ����
3m��m2��0��������3��2m��0��������
��m=1��
�����ABCD���ܳ�=��2m2+2m+6=6��
�ڡ߾���ABCD���ܳ�=��2m2+2m+6=��2��m2��m��+6=��2��m2��m+ ![]() ��
�� ![]() ��+6=��2��m��
��+6=��2��m�� ![]() ��2+
��2+ ![]() ��
��
�൱m= ![]() ʱ�������ֵ=
ʱ�������ֵ= ![]() ��
��
��m= ![]() ����y=��x2+3x��y=
����y=��x2+3x��y= ![]() ����A��������꣬
����A��������꣬
��ʱ��A������Ϊ�� ![]() ��
�� ![]() ����
����
�۵�����ABCD���ܳ�ȡ�����ֵʱ��m= ![]() ��
��
��ʱ����ABCD�����=ABBC=��3m��m2����3��2m��= ![]() ���������ֵ��
���������ֵ��
�ߵ�m= ![]() ʱ������ABCD�����=��3m��m2����3��2m��=1.6875��1.5=2.53125��
ʱ������ABCD�����=��3m��m2����3��2m��=1.6875��1.5=2.53125�� ![]() ��
��
�൱����ABCD���ܳ�ȡ�����ֵʱ�������������ͬʱȡ�����ֵ
����������1����֪�����߹�ԭ�㣬�������bֵ��������κ�������ʽ����2����A�������Ϊm���� ![]() ��m��0��AB=3m��m2 �� BC=3��2m������ABCD���ܳ�=��2m2+2m+6���ٸ����߶�AB��BC�ij�������������λ���ȼ�
��m��0��AB=3m��m2 �� BC=3��2m������ABCD���ܳ�=��2m2+2m+6���ٸ����߶�AB��BC�ij�������������λ���ȼ� ![]() ��m��0��ȷ��m��ֵ���Ӷ��������ABCD���ܳ����ڽ���2m2+2m+6�䷽�����ݶ��κ��������ʣ��ó�����ABCD���ܳ������ֵ���������ʱ��A�����ꣻ�۽�����ABCD���ܳ�ȡ�����ֵʱ��m��ֵ���������������ʽABBC=��3m��m2����3��2m���У��������ֵΪ2.5��Ȼ����
��m��0��ȷ��m��ֵ���Ӷ��������ABCD���ܳ����ڽ���2m2+2m+6�䷽�����ݶ��κ��������ʣ��ó�����ABCD���ܳ������ֵ���������ʱ��A�����ꣻ�۽�����ABCD���ܳ�ȡ�����ֵʱ��m��ֵ���������������ʽABBC=��3m��m2����3��2m���У��������ֵΪ2.5��Ȼ���� ![]() ��m��0�ķ�Χ���ҵ�һ��m=
��m��0�ķ�Χ���ҵ�һ��m= ![]() ʱ������ABCD�����=2.53125��
ʱ������ABCD�����=2.53125�� ![]() ���Ӷ��õ�������ABCD���ܳ�ȡ�����ֵʱ�������������ͬʱȡ�����ֵ��
���Ӷ��õ�������ABCD���ܳ�ȡ�����ֵʱ�������������ͬʱȡ�����ֵ��
�����㾫����������Ŀ����֪���������ö��κ�����ͼ������֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�