题目内容
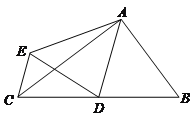
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
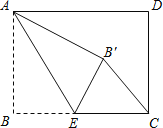
,![]() ,点D是BC的中点,将
,点D是BC的中点,将![]() 沿AD翻折得到
沿AD翻折得到![]() ,联结CE,那么线段CE的长等于_______.
,联结CE,那么线段CE的长等于_______.
【答案】![]()
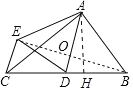
【解析】分析:如图连接BE交AD于O,作AH⊥BC于H.首先证明AD垂直平分线段BE,△BCE是直角三角形,求出BC、BE在Rt△BCE中,利用勾股定理即可解决问题.
详解:如图连接BE交AD于O,作AH⊥BC于H.
在Rt△ABC中,∵AC=4,AB=3,
∴BC=![]() =10,
=10,
∵CD=DB,
∴AD=DC=DB=5,
∵![]() BCAH=
BCAH=![]() ABAC,
ABAC,
∴AH=![]() ,
,
∵AE=AB,DE=DB=DC,
∴AD垂直平分线段BE,△BCE是直角三角形,
∵![]() ADBO=
ADBO=![]() BDAH,
BDAH,
∴OB=![]() ,
,
∴BE=2OB=![]() ,
,
在Rt△BCE中,EC=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
【题目】(10分)下面的图形是由边长为l的正方形按照某种规律排列而组成的.
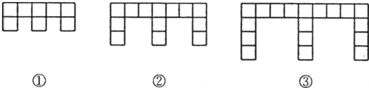
(1)观察图形,填写下表:
图形 | ① | ② | ③ |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .