题目内容
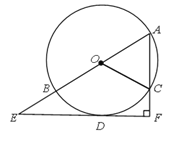
【题目】如图,AB是⊙O的直径,AC是弦,D是![]() 的中点,过点D作EF垂直于直线AC,垂足为F,交AB的延长线于点E.
的中点,过点D作EF垂直于直线AC,垂足为F,交AB的延长线于点E.
(1)求证:EF是⊙O的切线;
(2)若tanA=![]() ,AF=6,求⊙O的半径.
,AF=6,求⊙O的半径.
【答案】(1)见解析;(2)![]() .
.
【解析】分析:连接OD,由D是![]() 的中点得∠1=∠2,又∠A=
的中点得∠1=∠2,又∠A=![]() ∠BOC,故∠A=∠1,从而OD∥AF.易证∠EDO=∠F=90°.故可得结论;
∠BOC,故∠A=∠1,从而OD∥AF.易证∠EDO=∠F=90°.故可得结论;
(2)设⊙O半径为r,则OA=OD=OB=r.通过解直角三角形可得解.
详解:(1)如图1,连接OD.
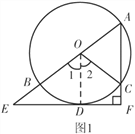
∵EF⊥AF,∴∠F=90°.
∵D是![]() 的中点,
的中点,
∴![]()
∴∠1=∠2=![]() ∠BOC.
∠BOC.
∵∠A=![]() ∠BOC, ∴∠A=∠1 .
∠BOC, ∴∠A=∠1 .
∴OD∥AF.
∴∠EDO=∠F=90°.
∴OD⊥EF.
∴EF是⊙O的切线.
(2)设⊙O半径为r,则OA=OD=OB=r.
在Rt△AFE中,tanA=![]() ,AF=6,
,AF=6,
∴EF=AF·tanA=8.
∴![]() .
.
∴OE=10-r.
∵cosA= ![]() ,
,
∴cos∠1= cos A=![]()
∴r =![]() , 即⊙O的半径为
, 即⊙O的半径为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
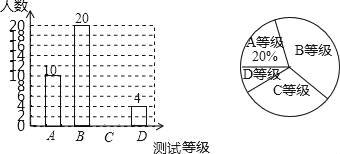
【题目】甲、乙两名射击选手在10次射击训练中的成绩统计图(部分)如图所示:
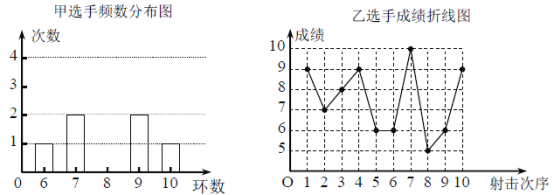
教练根据甲、乙两名射击选手的成绩绘制了如下数据分析表:
选手 | 平均数 | 中位数 | 众数 | 方差 |
甲 |
| 8 | 8 | c |
乙 | 7. 5 |
| 6和9 | 2. 65 |
根据以上信息,请解答下面的问题:
(1)补全甲选手10次成绩频数分布图;
(2)求![]() 的值;
的值;
(3)教练根据两名选手的10次成绩,决定选择甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).