Question

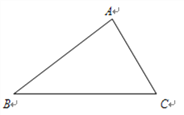
【题目】如图，在△ABC中，∠A=80°，∠B=40°．

(1)求作线段BC的垂直平分线DE，垂足为E，交AB于点D；(要求；尺规作图，保留作图痕迹，不写作法)

(2)在(1)的条件下，连接CD，求证：AC=CD．

Answer 1

【答案】(1)见解析;(2)见解析.

【解析】分析：（1）分别以A、B为圆心，大于AB长为半径画弧，两弧交于两点，过两点画直线，交AB于点E，交BC于点D；

（2）根据线段垂直平分线的性质得BD=CD，利用三角形的外角性质得∠2=80°，从而AC=DC，从而得出结论.

详解：（1）如图，直线DE为所求作的垂直平分线，点D，E就是所求作的点；

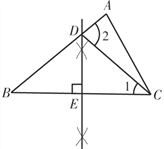
（2）连接CD.

∵DE垂直平分AB,

∴BD=CD，

∴∠1=∠B=40°.

∴∠2=∠B+∠1=80°，

∵∠A=80°,

∴∠2=∠A.

∴AC=CD.