题目内容
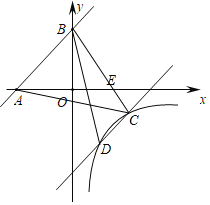
【题目】已知一次函数y=﹣x+m的图象与反比例函数![]() 的图象交于A、B两(点A在点B的左侧),点P为x轴上一动点,当有且只有一个点P,使得∠APB=90°,则m的值为_____.
的图象交于A、B两(点A在点B的左侧),点P为x轴上一动点,当有且只有一个点P,使得∠APB=90°,则m的值为_____.
【答案】4
【解析】
根据题意以AB为直径是圆与x轴相切于点P,根据直线的解析式即可证得△COD是等腰直角三角形,进而求得AB=m,根据平行线分线段成比例定理求得MC=BM=![]() m,即可求得B点的坐标,根据反比例函数图象上点的坐标特征得出
m,即可求得B点的坐标,根据反比例函数图象上点的坐标特征得出![]() m=2,解方程求得即可.
m=2,解方程求得即可.
设直线y=﹣x+m交x、y轴分别为C、D,
∴OD=OC=m,
∴△COD是等腰三角形,CD=![]() m,
m,
∴∠OCD=45°,
∵点P为x轴上一动点,有且只有一个点P,使得∠APB=90°,
∴以AB为直径是圆与x轴相切于点P,
设AB的中点为I,
∴IP⊥x轴,IA=IC=![]() m,
m,
∵I是CD的中点,
∴IP=![]() OD=
OD=![]() m,
m,
∴IB=![]() m,
m,
∴BC=IC﹣IB=![]() m,
m,
∵BM∥IP,
∴![]() ,即
,即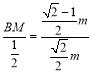
∴BM=![]() m
m
∵△BMC是等腰直角三角形,
∴MC=BM=![]() m,
m,
∴OM=m﹣![]() m=
m=![]() m,
m,
∴B(![]() ,
,![]() m),
m),
∵点B在反比例函数y=![]() 的图象上,
的图象上,
∴![]()
![]() m=2
m=2
解得m
故答案为4.

练习册系列答案
相关题目