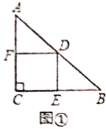题目内容
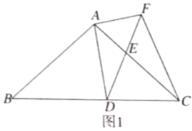
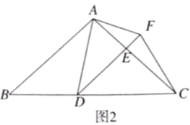
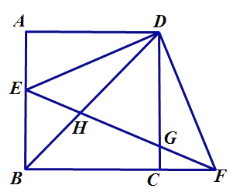
【题目】如图，正方形
的边长为
，点
在边
上，连接
，过点
作
，与
的延长线相交于点
，连接
，与边
相交于点
，与对角线
相交于点
．若
，则
的长为（ ）
A.
B.
C.
D.
【答案】C
【解析】
在正方形ABCD中，由FD与DE垂直，利用等式的性质得到一对角相等，再由一对直角相等，且AD=DC，利用AAS得到三角形DAE与三角形DCF全等，利用全等三角形对应边相等得到AE=CF，进而求出BE的长
∵在正方形ABCD中，∠BCD=90°，BC=CD=6，
∴BD=6
．
∵DF⊥DE，
∴∠ADE+∠EDC=90°，∠EDC+∠CDF=90°，
∴∠ADE=∠CDF，
在△ADE和△CDF中，
，
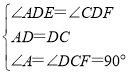∴△ADE≌△CDF（ASA），
∴AE=CF．
又∵BD=BF=6，
∴AE=CF=BF-BC=6-6，
∴BE=AB-AE=6-（6-6）=12-6，
即BE的长为12-6；
故选：C.
练习册系列答案
相关题目
