��Ŀ����
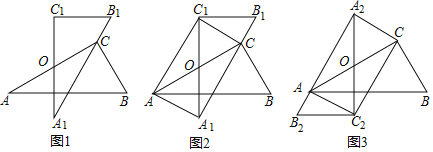
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬��BAC��30�㣬��O�DZ�AC���е㣮
��1����ͼ1�У�����ABC�Ƶ�O��ʱ����תn��õ���A1B1C1��ʹ��A1B1������C����n��ֵ��
��2����ͼ1����ƽ�Ƶ�ͼ2λ�ã���ͼ2�У�����AA1��AC1��CC1����֤���ı���AA1CC1�Ǿ��Σ�
��3����ͼ3�У�����ABC�Ƶ�O˳ʱ����תm��õ���A2B2C2��ʹ��A2B2������A������AC2��A2C��CC2��
������ֱ��д��m��ֵ���ı���AA2CC2����״��
����AB��![]() ����ֱ��д��AA2�ij���
����ֱ��д��AA2�ij���
���𰸡���1��n��60�㣻��2������������3����m��120�㣬�ı���AA2CC2�Ǿ��Σ���AA2��3![]() ��
��
��������
��1�����õ��������ε����������COC1���ɣ���2�����ݶԽ�����ȵ�ƽ���ı����Ǿ���֤�����ɣ���3���������COC2���ɣ����ݾ��ε��ж�֤�����ɽ�����⣮�ڽ�ֱ�����������A2C2�������AA2���ɣ�
��1���⣺��ͼ1�У�
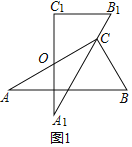
����ת��֪����A1B1C1�ա�ABC��
���A1����A��30����
��OC��OA��OA1��OA��
��OC��OA1��
���OCA1����A1��30����
���COC1����A1+OCA1��60����
��n��60����
��2��֤������ͼ2�У�
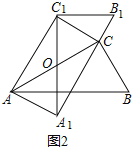
��OC��OA��OA1��OC1��
���ı���AA1CC1��ƽ���ı��Σ�
��OA��OA1��OC��OC1��
��AC��A1C1��
���ı���AA1CC1�Ǿ��Σ�
��3����ͼ3�У�
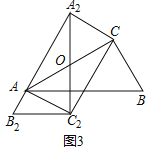
�١�OA��OA2��
���OAA2����OA2A��30����
���COC2����AOA2��180����30����30����120����
��m��120����
��OC��OA��OA2��OC2��
���ı���AA2CC2��ƽ���ı��Σ�
��OA��OA2��OC��OC2��
��AC��A2C2��
���ı���AA2CC2�Ǿ��Σ�
�ڡ�AC��A2C2��ABcos30����4![]() ��
��![]() ��6��
��6��
��AA2��A2C2cos30����6��![]() ��3
��3![]() ��
��

 ��������ϵ�д�
��������ϵ�д�����Ŀ��ijУ���к�����д������ѧϰ�Բ������������ͳ�ƣ����ݱ����ɼ��г�ͳ�Ʊ���������������ͳ��ͼ
��1���μӴ˴α�����ѧ����______________�ˣ�
��2��![]()
��3������һ�Ƚ��������ȡ����ѧ�����μ��м�������д������������״ͼ���б��ķ����������ѡ������ѧ������Ϊһ��һŮ�ĸ��ʣ�
�ȴ� | ���� | Ů�� |
һ�Ƚ� | 3 | m |
���Ƚ� | 6 | 12 |
���Ƚ� | 8 | 9 |
������ | 6 | n |

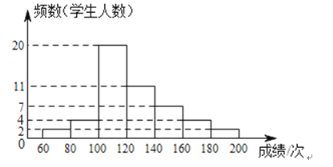
����Ŀ��ijѧУΪ�˽���꼶��ͬѧ1000���ܲ��ijɼ��������ȡ�˲����������в��ԣ��������Գɼ���ΪA��B��C��D�ĸ��ȼ��������˲������ijɼ��ȼ�Ƶ����������ͳ��ͼ��
�ɼ��ȼ� | Ƶ�� |
A | 24 |
B | 10 |
C | b |
D | 2 |
�ϼ� | a |
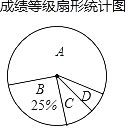
��1������a���� ����b���� ����
��2������ͼ��C��Բ�ĽǶ������� ����
��3������У���о��꼶����600�ˣ������û�л��A�ȼ���ѧ��������