��Ŀ����
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬B��5��0����MΪ��������OBCD�ױ�OB��һ�㣬OD=BC=2����DMC=��DOB=60�ȣ�
��1�����D��B����ֱ�ߵĺ�������ʽ��
��2�����M�����ꣻ
��3����DMC�Ƶ�M˳ʱ����ת����0�㣼����30��õ���D1MC1����D1��C1�������D��C��Ӧ���� ����MD1����DC�ڵ�E������MC1����CB�ڵ�F����DE=m��BF=n����m��n�ĺ�����ϵʽ��
����MD1����DC�ڵ�E������MC1����CB�ڵ�F����DE=m��BF=n����m��n�ĺ�����ϵʽ��
��1�����D��B����ֱ�ߵĺ�������ʽ��
��2�����M�����ꣻ
��3����DMC�Ƶ�M˳ʱ����ת����0�㣼����30��õ���D1MC1����D1��C1�������D��C��Ӧ����
 ����MD1����DC�ڵ�E������MC1����CB�ڵ�F����DE=m��BF=n����m��n�ĺ�����ϵʽ��
����MD1����DC�ڵ�E������MC1����CB�ڵ�F����DE=m��BF=n����m��n�ĺ�����ϵʽ����1������D��DA��OB������ΪA��
��Rt��ODA�У���DAO=90�㣬��DOB=60�㣬
��DA=OD•sin��DOB=
��
OA=OD•cos��DOB=1��
���D��������1��
����
��ֱ��DB�ĺ�������ʽΪy=kx+b��
��B��5��0����D��1��
������
��
���
��
��ֱ��DB�ĺ�������ʽΪy=-
x+
��
��2���ߡ�DMC=��DOB=60�㣬
���ODM+��DMO=120�㣬��DMO+��CMB=120�㣬
���ODM=��CMB��
�ߵ�������OBCD�ġ�DOB=��CBO��
���ODM����BMC��
��
=
=
��
��OD•BC=BM•OM��
��B����5��0����
��OB=5��
��OM=x����BM=5-x
��OD=BC=2��
��2��2=x��5-x����
���x1=1��x2=4��
��M��������1��0����4��0����
��3������M������Ϊ��1��0��ʱ����ͼ1��
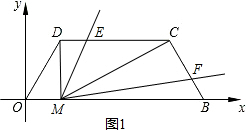 OM=1��BM=4��
OM=1��BM=4��
��DC��OB��
���MDE=��DMO��
�֡ߡ�DMO=��MCB��
���MDE=��MCB��
�ߡ�DME=��CMF=����
���DME����CMF��
��
=
=
=
=
��
��CF=2DE��
��CF=2-n��DE=m��
��2-n=2m����m=1-
��
����M������Ϊ��4��0��ʱ����ͼ2
 OM=4��BM=1��
OM=4��BM=1��
ͬ�����ɵá�DME����CMF��
��
=
=
=
=2��
��DE=2CF��
��CF=2-n��DE=m��
��m=2��2-n������m=4-2n��
����������m��n�ĺ�����ϵʽΪ��m=1-
��m=4-2n��

��Rt��ODA�У���DAO=90�㣬��DOB=60�㣬
��DA=OD•sin��DOB=
| 3 |
OA=OD•cos��DOB=1��
���D��������1��
| 3 |
��ֱ��DB�ĺ�������ʽΪy=kx+b��
��B��5��0����D��1��
| 3 |
|
���
|

��ֱ��DB�ĺ�������ʽΪy=-
| ||
| 4 |
| 5 |
| 4 |
| 3 |
��2���ߡ�DMC=��DOB=60�㣬
���ODM+��DMO=120�㣬��DMO+��CMB=120�㣬
���ODM=��CMB��
�ߵ�������OBCD�ġ�DOB=��CBO��
���ODM����BMC��
��
| OD |
| BM |
| OM |
| BC |
| DM |
| MC |
��OD•BC=BM•OM��
��B����5��0����
��OB=5��
��OM=x����BM=5-x
��OD=BC=2��
��2��2=x��5-x����
���x1=1��x2=4��
��M��������1��0����4��0����
��3������M������Ϊ��1��0��ʱ����ͼ1��
 OM=1��BM=4��
OM=1��BM=4����DC��OB��
���MDE=��DMO��
�֡ߡ�DMO=��MCB��
���MDE=��MCB��
�ߡ�DME=��CMF=����
���DME����CMF��
��
| DE |
| CF |
| DM |
| CM |
| OD |
| BM |
| 2 |
| 4 |
| 1 |
| 2 |
��CF=2DE��
��CF=2-n��DE=m��
��2-n=2m����m=1-
| n |
| 2 |
����M������Ϊ��4��0��ʱ����ͼ2
 OM=4��BM=1��
OM=4��BM=1��ͬ�����ɵá�DME����CMF��
��
| DE |
| CF |
| DM |
| CM |
| OD |
| BM |
| 2 |
| 1 |
��DE=2CF��
��CF=2-n��DE=m��
��m=2��2-n������m=4-2n��
����������m��n�ĺ�����ϵʽΪ��m=1-
| n |
| 2 |


��ϰ��ϵ�д�
 ������ϵ�д�
������ϵ�д� �żӾ���ϵ�д�
�żӾ���ϵ�д�
�����Ŀ
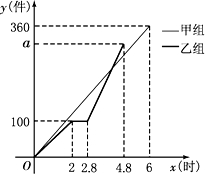


 ��1����λ/����ٶ��˶�����t��ʱ��P����ԲԲ��C�ľ���Ϊs����s��t�Ĺ�ϵʽ��
��1����λ/����ٶ��˶�����t��ʱ��P����ԲԲ��C�ľ���Ϊs����s��t�Ĺ�ϵʽ�� ͼ�ش��������⣺
ͼ�ش��������⣺
