题目内容
如图,直线y=
x-k分别与y轴、x轴相交于点A,点B,且AB=5,一个圆心在坐标原点,半径为1的圆,以0.8个单位/秒的速度向y轴正方向运动,设此动圆圆心离开坐标原点的时间为t(t≥0)(秒).
(1)求直线AB的解析式;
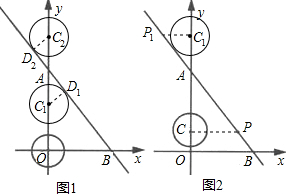
(2)如图1,t为何值时,动圆与直线AB相切;
(3)如图2,若在圆开始运动的同时,一动点P从B点出发,沿BA方向 以1个单位/秒的速度运动,设t秒时点P到动圆圆心C的距离为s,求s与t的关系式;
以1个单位/秒的速度运动,设t秒时点P到动圆圆心C的距离为s,求s与t的关系式;
(4)在(3)中,动点P自刚接触圆面起,经多长时间后离开了圆面?
| k |
| 3 |
(1)求直线AB的解析式;
(2)如图1,t为何值时,动圆与直线AB相切;
(3)如图2,若在圆开始运动的同时,一动点P从B点出发,沿BA方向
 以1个单位/秒的速度运动,设t秒时点P到动圆圆心C的距离为s,求s与t的关系式;
以1个单位/秒的速度运动,设t秒时点P到动圆圆心C的距离为s,求s与t的关系式;(4)在(3)中,动点P自刚接触圆面起,经多长时间后离开了圆面?
(1)由
x-k=0,k≠0,得x=3,
∴B点坐标为(3,0),
∵AB=5,
∴A点坐标为(0,4),
∴直线AB的解析式为y=-
x+4;
(2)设t秒时圆与AB相切,此时圆心为C1或C2,切点为D1,D2,如图所示,连接C1D1,C2D2,
由△AC1D1∽△ABO,得
=
,
即:
=
,
∴t=
,
同理由△AC2D2∽△ABO,
可求得t=
,
∴当t=
秒或
秒时,圆与直线AB相切;
(3)如图2,①当t=0时,s=3,
②当0<t<5时,设t秒时动圆圆心为C,连接PC.
=
=
=
,
∴PC∥OB,
∴
=
,即
=
,
∴s=-
t+3,
③当t=5时,s=0,
④当t>5时,设动圆圆心为C1,动点P在P1处,连接C1P1.
由②同理可知P1C1∥OB.
∴
=
,即s=
t-3,
又当t=0或5时,②中s=3或0,
所以综上所述:
当0≤t≤5时,s=-
t+3;
当t>5时,s=
t-3;
(4)当动点P与圆面刚接触时,或刚离开时,s=1,
当s=1时,由s=-
t+3,代入得t=
;
由s=
t-3,代入得t=
.
-
=
(秒),
∴动点P自刚接触圆面起,经
秒后离开了圆面.
| k |
| 3 |
∴B点坐标为(3,0),
∵AB=5,
∴A点坐标为(0,4),
∴直线AB的解析式为y=-
| 4 |
| 3 |
(2)设t秒时圆与AB相切,此时圆心为C1或C2,切点为D1,D2,如图所示,连接C1D1,C2D2,
由△AC1D1∽△ABO,得
| AC1 |
| AB |
| C1D1 |
| OB |
即:
| 4-0.8t |
| 5 |
| 1 |
| 3 |
∴t=
| 35 |
| 12 |
同理由△AC2D2∽△ABO,
可求得t=
| 85 |
| 12 |
∴当t=
| 35 |
| 12 |
| 85 |
| 12 |
(3)如图2,①当t=0时,s=3,
②当0<t<5时,设t秒时动圆圆心为C,连接PC.
| OC |
| BP |
| 0.8t |
| t |
| 4 |
| 5 |
| AO |
| AB |
∴PC∥OB,
∴
| PC |
| OB |
| AC |
| AO |
| s |
| 3 |
| 4-0.8t |
| 4 |
∴s=-
| 3 |
| 5 |
③当t=5时,s=0,
④当t>5时,设动圆圆心为C1,动点P在P1处,连接C1P1.
由②同理可知P1C1∥OB.
∴
| s |
| 3 |
| 0.8t-4 |
| 4 |
| 3 |
| 5 |
又当t=0或5时,②中s=3或0,
所以综上所述:
当0≤t≤5时,s=-
| 3 |
| 5 |
当t>5时,s=
| 3 |
| 5 |
(4)当动点P与圆面刚接触时,或刚离开时,s=1,
当s=1时,由s=-
| 3 |
| 5 |
| 10 |
| 3 |
由s=
| 3 |
| 5 |
| 20 |
| 3 |
| 20 |
| 3 |
| 10 |
| 3 |
| 10 |
| 3 |
∴动点P自刚接触圆面起,经
| 10 |
| 3 |


练习册系列答案
相关题目
 ,y)是直线y=kx+6上的一个动点.
,y)是直线y=kx+6上的一个动点.
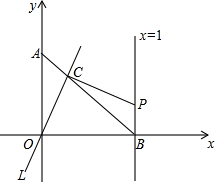
 射线MD1交边DC于点E,射线MC1交边CB于点F,设DE=m,BF=n.求m与n的函数关系式.
射线MD1交边DC于点E,射线MC1交边CB于点F,设DE=m,BF=n.求m与n的函数关系式. ,且半圆与y轴的交点D在射线AE的反向延长线上.
,且半圆与y轴的交点D在射线AE的反向延长线上.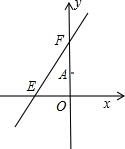 ,3).
,3).