题目内容
【题目】在△ABC中,AB=AC,DE∥BC. 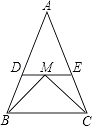
(1)试问△ADE是否是等腰三角形,说明理由;
(2)若M为DE上的点,且BM平分∠ABC,CM平分∠ACB,若△ADE的周长为20,BC=8.求△ABC的周长.
【答案】
(1)解:∵DE∥BC,
∴△ADE∽△ABC.
∴ ![]() =
= ![]() .
.
∵AB=AC,
∴AD=AE.
∴△ADE是等腰三角形
(2)解:∵DE∥BC,BM平分∠ABC,CM平分∠ACB,
∴∠MBC=∠DMB=∠DBM,∠MCB=∠MCE=∠EMC.
∴BD=DM,ME=CE.
∵△ADE的周长=AD+AE+DM+ME=20,
∴AD+AE+BD+CE=20.
∴△ABC的周长=(AD+AE+BD+CE)+BC=20+8=28
【解析】(1)由DE∥BC,可知△ADE∽△ABC,根据相似三角形性质即可求得结论;(2)由于DE∥BC,BM平分∠ABC,CM平分∠ACB,易证BD=DM,ME=CE,根据△ADE的周长为20,BC=8,即可求出△ABC的周长.
【考点精析】通过灵活运用平行线的性质和角平分线的性质定理,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上即可以解答此题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目