题目内容
【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
(3)若∠CDE=30°,OB=2,求![]() 的长.
的长.

【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】试题分析:(1)连接OD,BD,根据圆周角定理得到∠ABO=90°,根据等腰三角形的性质得到∠ABD=∠ADB,∠DBO=∠BDO,根据等式的性质得到∠ADO=∠ABO=90°,根据切线的判定定理即可得到即可;
(2)由AD是半圆O的切线得到∠ODE=90°,于是得到∠ODC+∠CDE=90°,根据圆周角定理得到∠ODC+∠BDO=90°,等量代换得到∠DOC=2∠BDO,∠DOC=2∠CDE即可得到结论;
(3)根据已知条件得到∠DOC=2∠CDE=54°,根据平角的定义得到∠BOD=180°-54°=126°,然后由弧长的公式即可计算出结果.
试题解析:(1)连接OD,BD,
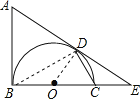
∵AB是⊙O的切线,∴AB⊥BC,即∠ABO=90°,
∵AB=AD,∴∠ABD=∠ADB,
∵OB=OD,∴∠DBO=∠BDO,
∴∠ABD+∠DBO=∠ADB+∠BDO,∴∠ADO=∠ABO=90°;
又∵OD是圆O的半径,∴AD是半圆O的切线;
(2)证明:由(1)知,∠ADO=∠ABO=90°,
∴∠A=360°-∠ADO-∠ABO-∠BOD=180°-∠BOD=∠COD
∵AD是半圆O的切线,∴∠ODE=90°,∴∠ODC+∠CDE=90°,
∵BC是⊙O的直径,∴∠ODC+∠BDO=90°,
∴∠BDO=∠CDE,
∵∠BDO=∠OBD,∴∠DOC=2∠BDO=2∠CDE,
∴∠A=2∠CDE;
(3)解:∵∠CDE=27°,∴∠DOC=2∠CDE=54°,∴∠BOD=180°-54°=126°,
∵OB=2,∴![]()

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案