��Ŀ����
����Ŀ����A��B��CΪ�����ϵ����㣬�����C�ڵ�A��B֮�䣬�ҵ���A�ľ����ǵ�C����B�ľ����3������ô���ǾͳƵ�C��{A��B}������㣮���磬��ͼ�٣���A��ʾ����Ϊ��3����B��ʾ����Ϊ1.��ʾ0�ĵ�C����A�ľ�����3������B�ľ�����1����ô��C��{A��B}������㣻���磬��ʾ��2�ĵ�D����A�ľ�����1������B�ľ�����3����ô��D�Ͳ���{A��B}����㣬����D��{B��A}������㣮
��֪ʶ���ã�
��ͼ�ڣ�M��NΪ�����ϵ����㣬��M����ʾ����Ϊ��2����N����ʾ����Ϊ6.
(1)��ʾ��_____�ĵ���{M��N}������㣻��ʾ��______�ĵ���{N��M}������㣻
(2)����P����ʾ����Ϊ3����P��{M��N}������㣬���M��N����ʾ���������Ǽ���M=______��N=_____(д��һ�鼴��)
(3)��ͼ�ۣ�A��BΪ�����ϵ����㣬��A����ʾ����Ϊ��10����B����ʾ����Ϊ50.����һ����P�ӵ�A���������˶�����P�˶��������ϵ�ʲôλ��ʱ��P��A��B��ǡ��һ����Ϊ�������������㣿

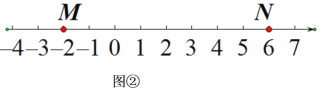
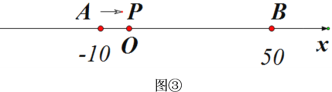
���𰸡���1��4��0����2��6��2����3��p��Ӧ������5��35��70��230.
��������
��1�����ݶ��巢�֣�������ʾ������{ M��N}�У�ǰ��ĵ�M�ǵ��������N�ľ����3�����Ӷ��ó����ۣ����ݶ��巢�֣�������ʾ������{N��M}�У�ǰ��ĵ�N�ǵ��������M�ľ����3�����Ӷ��ó����ۣ�
��2�����ݶ��壬���ɽ��;
��3����A����B�ľ���Ϊ60���������Ķ����������ۣ����Եó����ۣ�
(1)��6��(��2)��8��
��8��4��2��
��6��2��4��
���ʾ��4�ĵ���{M��N}�������
�ߣ�2��2��0.
���ʾ��0�ĵ���{N��M}������㣮
�ʴ�Ϊ:4��0
(2)��MΪ6����MP=3NP
��MP=3
��NP=1
��NΪ2
�ʴ�Ϊ:6��2
��3�����P��ʾ����Ϊx����10��x����
����A��ʾ����10����B��ʾ��50��
��AP��x������10����x+10��AB��50������10����60��
��P��B���Ҳ�ʱ��BP��x��50����P��B�����ʱ��BP��50��x
������P�ǣ�A��B�������������ʱ��
��AP��3BP��
��x+10��3��50-x����
��x��35��
������P�ǣ�B��A�������������ʱ��
��BP��3AP��
��50-x��3��x+10����
��x��5��
������B�ǣ�P��A�������������ʱ��
��BP��3AB��
��x��50��180��
��x��230��
������B�ǣ�A��P�������������ʱ��
��AB��3BP��
��60��3��x��50����
��x��70��
����p��Ӧ������5��35��70��230.

����Ŀ����ɽ�����ල�ִ�ijʳƷ�������Ĵ�װʳƷ�г����Ʒ20�������ÿ���������Ƿ���ϱ����ѳ�������IJ��ֱַ���������������ʾ����¼���±���
��������IJ�ֵ����λ���ˣ� | ��6 | ��2 | 0 | 1 | 3 | 4 |
���� | 1 | 4 | 3 | 4 | 5 | 3 |
��1����ÿ��ʳƷ�ı�����Ϊ450�ˣ����������20��ʳƷ���������Ƕ��ٿˣ�
��2��������ʳƷ�ĺϸ��Ϊ450��5�ˣ������ʳƷ�������ĺϸ��ʣ�