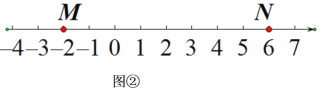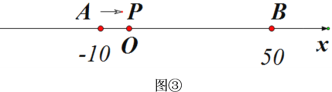��Ŀ����
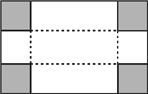
����Ŀ����֪������ABCD�У�AB=4cm��BC=8cm��AC�Ĵ�ֱƽ����EF�ֱ�AD��BC�ڵ�E��F������ΪO��
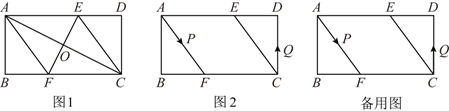
(1)��ͼ1������AF��CE��֤���ı���AFCEΪ���Σ�
(2)��ͼ1����AF�ij���
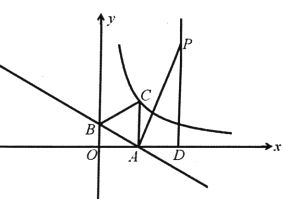
(3)��ͼ2������P��Q�ֱ��A��C����ͬʱ�������ء�AFB�͡�CDE���������˶�һ�ܣ�����P��A��F��B��Aֹͣ����Q��C��D��E��Cֹͣ�����˶������У���P���ٶ�Ϊÿ��1cm�����˶�ʱ��Ϊt�룮����Q���ٶ�Ϊÿ��0.8cm����A��P��C��Q�ĵ�Ϊ������ı�����ƽ���ı���ʱ����t��ֵ��
���𰸡���1������������2��AF=5cm����3��![]()
��������
��1�����ݾ��ε����ʡ�ƽ���ߵ����ʺ���֪��������ASA֤����AOE�ա�COF���ɵ�OE=OF�������ɵ��ı���AFCE��ƽ���ı��Σ�Ȼ����EF��AC����֤�ý��ۣ�
��2����AF=xcm������CF=xcm��BF=(8��x)cm��Ȼ����Rt��ABF�У��ɹ��ɶ�����������x�ķ��̣��ⷽ�̼��ý����
��3����Ϊ�����������һ��P��AF�ϣ���P��Q������ٶȼ��ɽ����жϣ��ڶ�����P��BF��ʱ��Q��CD��DE�ϣ�����ֻ�е�Q��DE��ʱ����A��P��C��Q�ĵ�Ϊ������ı��β��п�����ƽ���ı��Σ���ͼ���ú�t�Ĵ���ʽ�ֱ��ʾ��AQ��CP���Ӷ��ɵù���t�ķ��̣��ⷽ�̼��ý���������������P��AB��ʱ��Q��DE��CE�ϣ���P��Q�����λ�ü��ɽ����жϣ�
(1)֤�������ı���ABCD�Ǿ��Σ�
��AD��BC��
���EAO=��FCO��
��EF��AC�Ĵ�ֱƽ���ߣ�
��OA=OC��
�ߡ�AOE=��COF��
����AOE����COF��ASA����
��OE=OF��
��OA=OC��
���ı���AFCE��ƽ���ı��Σ�
��EF��AC��
��ƽ���ı���AFCE�����Σ�
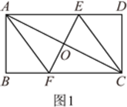
��2�����ı���AFCE�����Σ�
��AF=FC��
��AF=xcm����CF=xcm��BF=(8��x)cm��
���ı���ABCD�Ǿ��Σ����B=90����
����Rt��ABF�У��ɹ��ɶ����ã�![]() ��
��
��ã�x=5����AF=5cm��
(3)�����������
��һ��P��AF�ϣ���P���ٶ���1cm/s����Q���ٶ���0.8cm/s��
��Qֻ����CD�ϣ���ʱ��A��P��C��Q�ĵ�Ϊ������ı��β���ƽ���ı��Σ�
�ڶ�����P��BF��ʱ��Q��CD��DE�ϣ�����ֻ�е�Q��DE��ʱ����A��P��C��Q�ĵ�Ϊ������ı��β��п�����ƽ���ı��Σ���ͼ��
��AQ=8��(0.8t��4)��CP=5+(t��5)��
��8��(0.8t��4)=5+(t��5)��
��ã�![]() ��
��
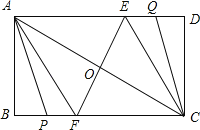
�����������P��AB��ʱ��Q��DE��CE�ϣ���ʱ��A��P��C��Q�ĵ�Ϊ������ı��β���ƽ���ı��Σ�
������������![]() ʱ����A��P��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�
ʱ����A��P��C��Q�ĵ�Ϊ������ı�����ƽ���ı��Σ�