Question

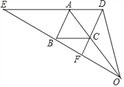
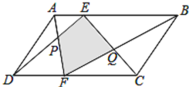
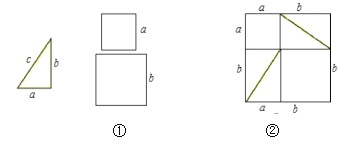
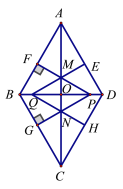
【题目】如图：菱形ABCD的对角线AC，BD相交于点O，AC= ，BD=，动点P在线段BD上从点B向点D运动，PF⊥AB于点F，PG⊥BC于点G，四边形QEDH与四边形PFBG关于点O中心对称，设菱形ABCD被这两个四边形盖住部分的面积为S1，未被盖住部分的面积为S2，，若S1=S2，则的值是（　　）

A. B. 或C. D. 不存在

Answer 1

【答案】A

【解析】

根据对称性确定E、F、G、H都在菱形的边上，由于点P在BO上与点P在OD上求S1和S2的方法不同，因此需分情况讨论，由S1=S2和S1+S2=8可以求出S1=S2=4．然后在两种情况下分别建立关于x的方程，解方程，结合不同情况下x的范围确定x的值．

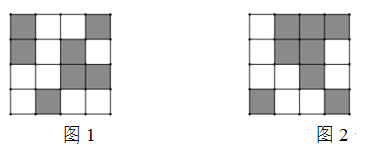
①当点P在BO上，0＜x≤2时，如图1所示．

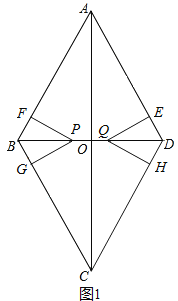
∵四边形ABCD是菱形，AC=4，BD=4，

∴AC⊥BD，BO=BD=2，AO=AC=2，

且S菱形ABCD=BDAC=8．

∴tan∠ABO==．

∴∠ABO=60°．

在Rt△BFP中，

∵∠BFP=90°，∠FBP=60°，BP=x，

∴sin∠FBP=．

∴FP=x．

∴BF=．

∵四边形PFBG关于BD对称，

四边形QEDH与四边形PEBG关于AC对称，

∴S△BFP=S△BGP=S△DEQ=S△DHQ．

∴S1=4S△BFP

=4××x

=x2．

∴S2=8-x2．

②当点P在OD上，2＜x≤4时，如图2所示．

∵AB=4，BF=，

∴AF=AB-BF=4．

在Rt△AFM中，

∵∠AFM=90°，∠FAM=30°，AF=4-．

∴tan∠FAM=．

∴FM=（4-）．

∴S△AFM=AFFM

=（4-）（4-）

=（4-）2．

∵四边形PFBG关于BD对称，

四边形QEDH与四边形FPBG关于AC对称，

∴S△AFM=S△AEM=S△CHN=S△CGN．

∴S2=4S△AFM

=4×（4-）2

=（x-8）2．

∴S1=8-S2=8-（x-8）2．

综上所述：

当0＜x≤2时，S1=x2，S2=8-x2；

当2＜x≤4时，S1=8-（x-8）2，S2=（x-8）2．

当点P在BO上时，0＜x≤2．

∵S1=S2，S1+S2=8，

∴S1=4．

∴S1=x2=4．

解得：x1=2，x2=-2．

∵2＞2，-2＜0，

∴当点P在BO上时，S1=S2的情况不存在．

当点P在OD上时，2＜x≤4．

∵S1=S2，S1+S2=8，

∴S2=4．

∴S2=（x-8）2=4．

解得：x1=8+2，x2=8-2．

∵8+2＞4，2＜8-2＜4，

∴x=8-2．

综上所述：若S1=S2，则x的值为8-2．

故选A.