题目内容
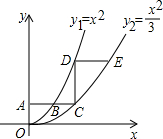
如图,平行于x轴的直线AC分别交抛物线y1=x2(x≥0)与 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 = .
= .
 (x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则
(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E,则 = .
= .
 .
.试题分析:设A点坐标为(0,a),(a>0),
则由x2=a,解得x=
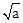 ,∴点B(
,∴点B(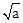 ,a);由
,a);由 ,解得x=
,解得x= ,∴点C(
,∴点C( ,a).
,a).∴BC=

∵CD∥y轴,∴点D的横坐标与点C的横坐标相同,为
 . ∴y1=
. ∴y1= ="3a."
="3a." ∴点D的坐标为(
 ,3a).
,3a).∵DE∥AC,∴点E的纵坐标为3a. ∴由
 解得x=
解得x=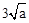 .∴点E的坐标为(
.∴点E的坐标为(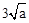 ,3a)。
,3a)。∴DE=
 .
.∴
 .
.
练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 ,请你化成
,请你化成 的形式,并在直角坐标系中画出
的形式,并在直角坐标系中画出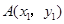 ,
,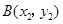 是(1)中图象上的两点,且
是(1)中图象上的两点,且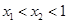 ,请直接写出
,请直接写出 、
、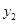 的大小关系;
的大小关系;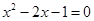 的根来,要求保留画图痕迹,说明结果.
的根来,要求保留画图痕迹,说明结果.
 与y轴交于(0,3),
与y轴交于(0,3), 经过点A(4,0),B(2,2),连结OB,AB.
经过点A(4,0),B(2,2),连结OB,AB.
 、
、 的值;
的值;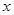 元,每售出一个小家电可获得的利润是多少元?(用含
元,每售出一个小家电可获得的利润是多少元?(用含 与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上.
与该二次函数交于A,B两点,其中A点(3,4),B点在y轴上.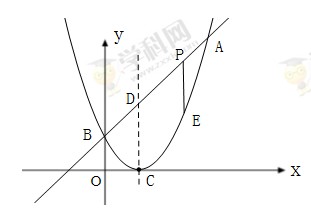
 (a≠0)中的自变量x与函数值y的部分对应值如下表:
(a≠0)中的自变量x与函数值y的部分对应值如下表: 的解为 .
的解为 . 的图象可能是( )
的图象可能是( )