题目内容
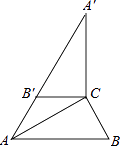
【题目】如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上,
求证:AE2+AD2=2AC2 . 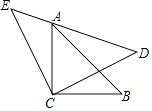
【答案】证明:连接BD, 
∵△ACB和△ECD都是等腰直角三角形
∴∠ACB=∠ECD=90°,AC=BC,EC=DC,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
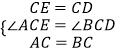 ,
,
∴△ACE≌△BCD(SAS)
∴BD=AE,∠BDC=∠E,
∵∠E+∠CDE=90°,
∴∠BDC+∠CDE=90°,
即∠ADB=90°,
在Rt△ADB中,BD2+AD2=AB2,
∵AB2=2AC2,
∴AE2+AD2=2AC2.
【解析】连接BD,根据等腰直角三角形的性质得出∠ACB=∠ECD=90°,AC=BC,EC=DC,进而得出∠ACE=∠BCD,,然后利用SAS判断出△ACE≌△BCD,根据全等三角形的性质得出BD=AE,∠BDC=∠E,从而得出∠ADB=90°,然后利用勾股定理及等量代换得出结论。
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
相关题目