题目内容
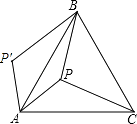
【题目】如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE. 
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.
【答案】
(1)证明:∵将△ABD绕点A逆时针旋转60°得△ACE
∴△ABD≌△ACE,∠BAC=∠DAE,
∴AD=AE,BD=CE,∠AEC=∠ADB=120°,
∵△ABC为等边三角形
∴∠BAC=60°
∴∠DAE=60°
∴△ADE为等边三角形,
∴AD=DE
(2)∠ADC=90°,∠AEC=120°,∠DAE=60°
∴∠DCE=360°﹣∠ADC﹣∠AEC﹣∠DAE=90°
(3)∵△ADE为等边三角形
∴∠ADE=60°
∴∠CDE=∠ADC﹣∠ADE=30°
又∵∠DCE=90°
∴DE=2CE=2BD=2,
∴AD=DE=2
在Rt△DCE中, ![]()
【解析】(1)利用旋转的性质和等边三角形的性质先判断出△ADE是等边三角形即可;(2)利用四边形的内角和即可求出结论;(3)先求出CD,再用勾股定理即可求出结论.
【考点精析】利用等腰三角形的性质和等边三角形的性质对题目进行判断即可得到答案,需要熟知等腰三角形的两个底角相等(简称:等边对等角);等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
相关题目