题目内容
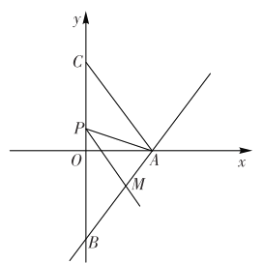
【题目】如图,已知直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 将
将![]() 沿
沿![]() 轴折叠,使点
轴折叠,使点![]() 落在
落在![]() 轴的点
轴的点![]() 上,设
上,设![]() 为线段
为线段![]() 上的一个动点,点
上的一个动点,点![]() 与点
与点![]() 不重合,连接
不重合,连接![]() .以点
.以点![]() 为端点作射线
为端点作射线![]() 交线段
交线段![]() 于点
于点![]() 使
使![]() .
.
![]() 求点
求点![]() 的坐标;
的坐标;
![]() 当
当![]() 时,求直线
时,求直线![]() 的解析式;
的解析式;
![]() 是否存在点
是否存在点![]() 使
使![]() 为直角三角形?若存在,请直接写出点
为直角三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() ,
,![]() .
.
【解析】
(1)先利用待定系数法求得函数关系式,进而求得点B坐标,再利用对称性求得C的坐标即可;
(2)先利用轴对称性及三角形的外角性质证得![]() ,再根据勾股定理求得AC长,利用“ASA”可证得
,再根据勾股定理求得AC长,利用“ASA”可证得![]() ,进而可求得BM,AM的长,过点
,进而可求得BM,AM的长,过点![]() 作
作![]() 轴于点
轴于点![]() ,由此可得
,由此可得![]() ,利用相似三角形的性质可求得点M的坐标,最后利用待定系数法即可求得直线CM的函数关系式;
,利用相似三角形的性质可求得点M的坐标,最后利用待定系数法即可求得直线CM的函数关系式;
(3)分类讨论,当![]() 时,则有
时,则有![]() ,利用相似三角形的性质可求得点
,利用相似三角形的性质可求得点![]() 的坐标,当
的坐标,当![]() 时,则
时,则![]() ,进而可证得
,进而可证得![]() ,再根据过点
,再根据过点![]() 只有一条直线与
只有一条直线与![]() 垂直,即可求得此时的点
垂直,即可求得此时的点![]() 的坐标为
的坐标为![]()
解:(1)∵直线![]() 与
与![]() 轴相交于点
轴相交于点![]()
∴![]()
![]()
![]() 直线的解析式为
直线的解析式为![]()
令![]() 则
则![]()
![]()
![]() 点
点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,
![]()
(2)∵点![]() 与点
与点![]() 关于
关于![]() 轴对称
轴对称
![]()
![]()
![]()
![]()
![]()
![]()
在△PAC与△MPB中,
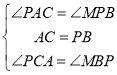
![]() (ASA)
(ASA)
![]()
![]()
过点![]() 作
作![]() 轴于点
轴于点![]() .
.
![]()
![]()
![]() ,
,![]()
![]()
![]() 点
点![]() 的坐标是
的坐标是![]()
又点![]() 的坐标为
的坐标为![]()
设直线CM为![]() ,
,
则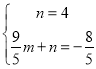 ,
,
解得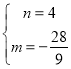
![]() 直线
直线![]() 的解析式为
的解析式为![]() ;
;
(3)存在,![]() ,
,![]()
由题意,得![]()
当![]() 时,则有
时,则有![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
当![]() 时,则
时,则![]()
![]()
![]()
![]()
![]()
![]() 过点
过点![]() 只有一条直线与
只有一条直线与![]() 垂直,
垂直,
![]() 此时点
此时点![]() 与点
与点![]() 重合,即符合条件的点
重合,即符合条件的点![]() 的坐标为
的坐标为![]()
![]() 使
使![]() 为直角三角形的点
为直角三角形的点![]() 有两个,
有两个,![]() ,
,![]()

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案【题目】某公司为了宣传一种新产品,在某地先后举行![]() 场产品促销会,已知该产品每台成本为
场产品促销会,已知该产品每台成本为![]() 万元,设第
万元,设第![]() 场产品的销售量为
场产品的销售量为![]() (台),在销售过程中获得以下信息:
(台),在销售过程中获得以下信息:
信息1:已知第一场销售产品![]() 台,然后每增加一场,产品就少卖出
台,然后每增加一场,产品就少卖出![]() 台;
台;
信息2:产品的每场销售单价![]() (万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次
(万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次![]() 成正比,第21场--第40场浮动价与销售场次
成正比,第21场--第40场浮动价与销售场次![]() 成反比,经过统计,得到如下数据:
成反比,经过统计,得到如下数据:
| 3 | 10 | 25 |
| 10.6 | 12 | 14.2 |
(1)求![]() 与
与![]() 之间满足的函数关系式;
之间满足的函数关系式;
(2)当产品销售单价为13万元时,求销售场次是第几场?
(3)在这![]() 场产品促销会中,哪一场获得的利润最大,最大利润是多少?
场产品促销会中,哪一场获得的利润最大,最大利润是多少?