题目内容
【题目】如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得到折痕EC;将∠AEF对折,点A落在直线EF上的点A′处,得到折痕EN.
(1)若∠BEB′=110°,则∠BEC= °,∠AEN= °,∠BEC+∠AEN= °.
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.
(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠AEN的度数.(提示,长方形的四个角都是90°)
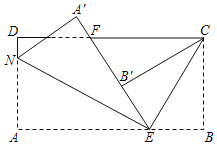
【答案】(1)55,35,90;(2)不改变,理由见解析;(3)∠AEN=30°
【解析】
(1)由对折的定义∠BEC=∠B'EC=![]() ∠BEB'=55°,∠AEN=∠A'EN=
∠BEB'=55°,∠AEN=∠A'EN=![]() ∠AEA'=
∠AEA'=![]() (180°﹣110°)=35°,得出∠BEC+∠AEN=90°即可;
(180°﹣110°)=35°,得出∠BEC+∠AEN=90°即可;
(2)同(1)得出∠BEC=∠B'EC=![]() ∠BEB',∠AEN=∠A'EN=
∠BEB',∠AEN=∠A'EN=![]() ∠AEA',得出∠BEC+∠AEN=
∠AEA',得出∠BEC+∠AEN=![]() ∠BEB'+
∠BEB'+![]() (180°﹣∠BEB')=90°;
(180°﹣∠BEB')=90°;
(3)由长方形的定义得出∠BCE+∠ECB′+∠B′CF=90°,由对折得出∠BCE=∠ECB′=∠B′CF=30°,求出∠FCE=60°,由平行线的性质得出∠BEC=∠FCE=60°,由(2)得出∠BEC+∠AEN=90°,即可得出答案.
解:(1)∵将∠BEF对折,点B落在直线EF上的点B′处,得到折痕EC;将∠AEF对折,点A落在直线EF上的点A′处,得到折痕EN.
∴∠BEC=∠B'EC=![]() ∠BEB'=55°,∠AEN=∠A'EN=
∠BEB'=55°,∠AEN=∠A'EN=![]() ∠AEA'=
∠AEA'=![]() (180°﹣110°)=35°,
(180°﹣110°)=35°,
∴∠BEC+∠AEN=90°,
故答案为:55,35,90;
(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值不改变,理由如下:
同(1)得:∠BEC=∠B'EC=![]() ∠BEB',∠AEN=∠A'EN=
∠BEB',∠AEN=∠A'EN=![]() ∠AEA',
∠AEA',
∴∠BEC+∠AEN=![]() ∠BEB'+
∠BEB'+![]() (180°﹣∠BEB')=90°;
(180°﹣∠BEB')=90°;
(3)∵长方形纸片ABCD,
∴AB∥CD,∠BCD=90°,
∴∠BCE+∠ECB′+∠B′CF=90°,
∵将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,
∴∠BCE=∠ECB′=∠B′CF=30°,
∴∠FCE=60°,
∵AB∥CD,
∴∠BEC=∠FCE=60°,
由(2)得:∠BEC+∠AEN=90°,
∴∠AEN=90°﹣∠BEC=90°﹣60°=30°.

 阅读快车系列答案
阅读快车系列答案