��Ŀ����
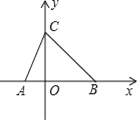
����Ŀ����ͼ1����Rt��ACB�У���BAC=90����AB=AC���ֱ��B��C����������A��ֱ��l�Ĵ��ߣ�����ΪD��E��
��1����ͼ1����D��E������ֱ��BC��ͬ��ʱ�����룬BD��CE��DE�����߶���������������ϵ����˵�����ɣ�
��2����ͼ��2��������1���е�������Ϊ������ABC�У�AB=AC��D��A��E���㶼��ֱ��m�ϣ���������BDA=��AEC=��BAC=����������Ϊ������ǻ�۽ǣ����ʽ���DE=BD+CE�Ƿ��������������������֤����������������˵�����ɣ�

��3����ͼ3����BAC=90����AB=25��AC=35����P��B�������B��A��C·�����յ�C�˶�����Q��C�������C��A��B·�����յ�B�˶�����P��Q�ֱ���ÿ��2��3����λ���ٶ�ͬʱ��ʼ�˶���ֻҪ��һ�㵽����Ӧ���յ�ʱ����ͬʱֹͣ�˶������˶������У��ֱ��P��Q��PF��l��F��QG��l��G���ʣ���P�˶�������ʱ����PFA����QAGȫ�ȣ���ֱ��д���𰸣�
���𰸡�(1)BD+ CE = DE�� (2)��������3����P�˶�10��12��.
�������������������1��)BD+ CE = DE�����ݡ�BDA=��CEA=90����֤�á�EAC=��ABD������AAS֤����ABD�ա�ACE������ȫ�������ε����ʿɵ�AD=CE��BD=AE������DE=BD+CE��
��2�����������á�BDA=��BAC=�������DBA+��BAD=��BAD+��CAE=180��-�����ó���CAE=��ABD������֤����ADB�ա�CEA�����ɵó��𰸣�
��3�����������ε������ʽ������ã�
��4����֤��PFA=��QGA����PAF=��AQG��ֻ��PA=QA���Ϳɵõ���PFA���QAGȫ�ȣ�Ȼ��ֻ����ݵ�P�͵�Q��ͬλ�ý��з������ۼ��ɽ�����⣮
���������
(1)BD+DE=CE
֤����BD��ֱ��l��CE��ֱ��l��
��BD��l��CE��l
���BDA=��CEA=90��
���ABD+��DAB=90��
�ߡ�BAC=90��
���DAB+��CAE=90��
���ABD=��CAE
�ڡ�ABD�͡�CAE�У�
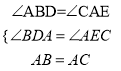
���ABD�ա�CAE��AAS����
��AD=CE��BD=AE��
��DE=AD+AE��
��DE=CE+BD��
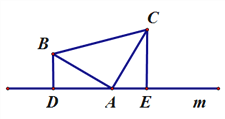
(2)����
֤���ߡ�CAE=180��-��BAC-��BAD
��DBA=180��-��BDA-��BAD
�ߡ�BAC=��BDA
���CAE=��ABD
�ڡ�ABD�͡�CAE�У�
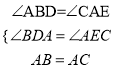
���ABD�ա�CAE��AAS����
��AD=CE��BD=AE��
��DE=AD+AE��
��DE=CE+BD��

��3����P�˶�10��12��.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�