题目内容
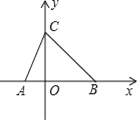
【题目】如图,点A为x轴负半轴上一点,点B为x轴正半轴上一点,OA、OB(OA<0B)的长分别是关于x的一元二次方程x2﹣4mx+m2+2=0的两根,C(0,3),且△ABC的面积为6,求∠ABC的度数.
【答案】∠ABC=45°.
【解析】试题分析:先根据三角形ABC的面积求出AB的值,再由根与系数的关系就可以求出m的值,从而求出方程的解,就可以得出OB的值,进而得出△OBC为等腰直角三角形就可以得出结论.
试题解析:∵C(0,3),
∴CO=3.
∵△ABC的面积为6,
∴![]() =6,∴AB=4,
=6,∴AB=4,
∵OA、OB(OA<0B)的长分别是关于x的一元二次方程x2﹣4mx+m2+2=0的两根,
∴OA+OB=4m,∴4m=4,∴m=1,
∴一元二次方程为:x2﹣4x+3=0,∴x1=1,x2=3,
∵OA<0B,∴OA=1,OB=3.∴OB=OC,
∴△OBC是等腰直角三角形,
∴∠ABC=45°,
答:∠ABC=45°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目