题目内容
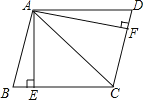
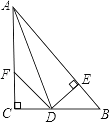
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF;
求证:(1)CF=EB.
(2)AB=AF+2EB.
【答案】(1)见解析;(2)见解析.
【解析】
(1)利用HL证明RT△CDF≌RT△EDB即可得出CF=EB;
(2)利用HL证明RT△ADE≌RT△ADC即可得出AC=AE,再由AB=AE+EB=AF+CF+EB进行等量代换即可.
(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△CDF和Rt△EDB中,
![]() ,
,
∴Rt△CDF≌Rt△EDB(HL)
∴CF=EB
(2)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC,
∴CD=DE.
在△ADC与△ADE中,![]() ,
,
∴△ADC≌△ADE(HL),
∴AC=AE,∴AB=AE+BE=AC+EB=AF+CF+EB=AF+2EB.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
【题目】从甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,对两人进行了五次模拟,并对成绩(单位:分)进行了整理,计算出![]() =83分,
=83分,![]() =82分,绘制成如下尚不完整的统计图表.
=82分,绘制成如下尚不完整的统计图表.
甲、乙两人模拟成绩统计表
① | ② | ③ | ④ | ⑤ | |
甲成绩/分 | 79 | 86 | 82 | a | 83 |
乙成绩/分 | 88 | 79 | 90 | 81 | 72 |
根据以上信息,回答下列问题:
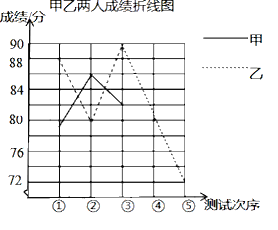
(1)a=
(2)请完成图中表示甲成绩变化情况的折线.
(3)经计算S甲2=6,S乙2=42,综合分析,你认为选拔谁参加比赛更合适,说明理由.
(4)如果分别从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于82分的概率.