题目内容
【题目】如图，△ABC为等边三角形，点D，E分别在BC，AC边上，且AE＝CD，AD，BE相交于点P，BQ⊥AD于Q，PQ＝3，PE＝1.
(1)求证：△ABE≌△CAD；
(2) 求BE的长
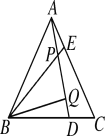
【答案】（1）证明见解析；（2）7
【解析】
（1）根据AE=CD，AB=AC，∠BAC=∠C即可求得△ABE≌△CAD；
（2）由（1）得∠AEB=∠ADC，即可求得∠BPQ=∠C，即可求得BP的长，即可解题．
（1）∵△ABC是等边三角形，
∴AB=BC=AC，
∴∠BAC=∠C=60°，
∵AB=AC，AE=CD，
∴△ADC≌△BEA，
（2）∵△ADC≌△BEA，
∴∠ABE=∠CAD，
∵∠CAD+∠BAD=60°，
∴∠ABE+∠BAD=60°，
∴∠BPQ=60°，
∵BQ⊥AD，
∴∠PBQ=30°，
∴BP=2PQ，
∴BP=6，
∴BE=BP+PE=6+1=7.
练习册系列答案
相关题目
【题目】有A、B两种饮料，这两种饮料的体积和单价如表：
类型 | A | B |
单瓶饮料体积/升 | 1 | 2.5 |
单价/元 | 3 | 4 |
（1）小明购买A、B两种饮料共13升，用了25元，他购买A，B两种饮料个各多少瓶？
（2）若购买A、B两种饮料共36瓶，且A种饮料的数量不多于B种饮料的数量，则最少可以购买多少升饮料？
