题目内容
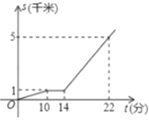
【题目】黄岩岛是我国南沙群岛的一个小岛，渔产丰富．一天某渔船离开港口前往该海域捕鱼．捕捞一段时间后，发现一外国舰艇进入我国水域向黄岩岛驶来，渔船向渔政部门报告，并。立即返航．渔政船接到报告后，立即从该港口出发赶往黄岩岛．下图是渔政船及渔船与港口的距离s和渔船离开港口的时间t之间的函数图象．(假设渔船与渔政船沿同一航线航行)
(1)直接写出渔船离开港口的距离s和渔船离开港口的时间t之间的函数关系式
(2)求渔船与渔政船相遇对，两船与黄岩岛的距离、
(3在渔政船驶往黄岩岛的过程中，求渔船从港口 出发经过多长时间与渔政船相距30海里?
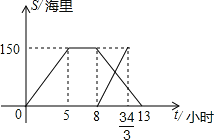
【答案】（1）当0≤t≤5时，s=30t；当5＜t≤8时，s=150；当8＜t≤13时，s=－30t＋390（2）=60海里（3）9.6小时或10.5小时
【解析】解：（1）当0≤t≤5时，s=30t；当5＜t≤8时，s=150；当8＜t≤13时，s=－30t＋390。
（2）设渔政船离港口的距离s与渔船离开港口的时间t之间的函数关系式为s=kt+b，则
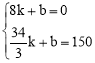，解得
。∴s=45t－360。
联立
，解得
。
∴渔船离黄岩岛的距离为150－90=60（海里）。
（3）∵
，∴分两种情况：
①－30t＋390－（45t－360）=30，解得t=9.6；
②45t－360－（－30t＋390）=30，解得t=10.5。
∴当渔船离开港口9.6小时或10.5小时时，两船相距30海里。
（1）由图象可得出渔船离港口的距离s和它离开港口的时间t的函数关系式，分为三段求函数关系式。
（2）由图象可知，当8＜t≤13时，渔船和渔政船相遇，利用待定系数求渔政船的函数关系式，再与这个时间段渔船的函数关系式联立，可求相遇时，离港口的距离，再求两船与黄岩岛的距离。
（3）在渔政船驶往黄岩岛的过程中，8＜t≤13，渔船与渔政船相距30海里，有两种可能：
①s渔－s渔政=30，②s渔政－s渔=30，将函数关系式代入，列方程求t。
