题目内容
【题目】根据下列已知条件,分别指出两个图形中的等腰三角形,并利用第一个图证明结论。
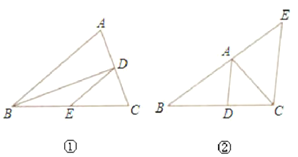
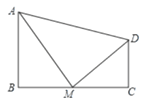
(1)如图①,BD平分∠ABC,DE//AB
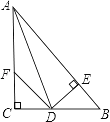
(2) 如图②,AD平分∠BAC , EC//AD
【答案】(1)△BDE是等腰三角形,理由见解析;(2)△ACE是等腰三角形,理由见解析;
【解析】
(1)根据角平分线的性质和平行线的性质,即可解答;
(2)根据角平分线的性质和平行线的性质,即可解答;
(1)△BDE是等腰三角形,理由如下:
∵BD平分∠ABC,
∴∠ABD=∠CBD.
∵DE∥AB,
∴∠BDE=∠ABD.
∴∠BDE=∠CBD.
∴△BDE是等腰三角形(有两个角相等的三角形是等腰三角形).
(2)△ACE是等腰三角形,理由如下:
∵AD平分∠BAC,
∴∠BAD=∠CAD.
∵EC∥AD,
∴∠BAD=∠BEC,∠DAC=∠ACE.
∴∠BEC=∠ACE.
∴△ACE是等腰三角形(有两个角相等的三角形是等腰三角形).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
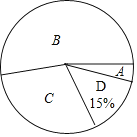
【题目】某市将开展以“走进中国数学史”为主题的知识凳赛活动,红树林学校对本校100名参加选拔赛的同学的成绩按A,B,C,D四个等级进行统计,绘制成如下不完整的统计表和扇形统计图:
成绩等级 | 频数(人数) | 频率 |
A | 4 | 0.04 |
B | m | 0.51 |
C | n | |
D | ||
合计 | 100 | 1 |
(1)求m= ,n= ;
(2)在扇形统计图中,求“C等级”所对应心角的度数;
(3)成绩等级为A的4名同学中有1名男生和3名女生,现从中随机挑选2名同学代表学校参加全市比赛,请用树状图法或者列表法求出恰好选中“1男1女”的概率.