Question

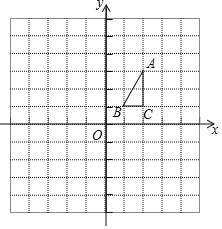
【题目】如图已知A1，A2，A3，…An是x轴上的点，且OA1=A1A2=A2A3=A3A4=…=An-1An=1，分别过点A1，A2，A3，…An′作x轴的垂线交二次函数（x＞0）的图象于点P1，P2，P3，…Pn，若记△OA1P1的面积为S1，过点P1作P1B1⊥A2P2于点B1，记△P1B1P2的面积为S2，过点P2作P2B2⊥A3P3于点B2，记△P2B2P3的面积为S3，…依次进行下去，最后记△Pn-1Bn-1Pn（n＞1）的面积为Sn，则Sn=（ ）

A. B. C. D.

Answer 1

【答案】A

【解析】

根据二次函数上点的特征，求得当x=n和x=n-1时y的值，再利用三角形的面积公式求解即可.

二次函数y=x2，由图象知：

当x=n时，y=n2，

当x=n-1时，y=（n-1）2，

∴Sn=×1×[n2-（n-1）2]=．

故选A．