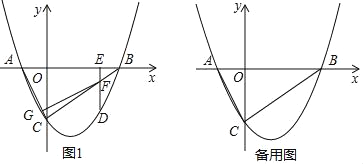
题目内容
【题目】如图,在![]() 和
和![]() 中,
中,![]() ,点
,点![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,点
,点![]() 、
、![]() 关于
关于![]() 成轴对称,连接
成轴对称,连接![]() 、
、![]() .
.
(1)求证:![]() 为等边三角形;
为等边三角形;
(2)连接![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接DE、CE,根据“直角三角形斜边上的中线等于斜边的一半”可得DE=CE=![]() AB=4,再由CD=4可证明△CDE是等边三角形,再由点
AB=4,再由CD=4可证明△CDE是等边三角形,再由点![]() 、
、![]() 关于
关于![]() 成轴对称可得结论;
成轴对称可得结论;
(2)由点![]() 、
、![]() 关于
关于![]() 成轴对称,只要求得FG的长得出结论.
成轴对称,只要求得FG的长得出结论.
(1)连接DE、CE,
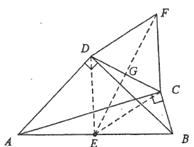
∵∠ADB=∠ACB=90°,点E为AB的中点,
∴DE=CE=![]() AB,
AB,
∵CD=4 ,AB=8,
∴CD=![]() AB,
AB,
∴DE=CE=CD,
∵点![]() 、
、![]() 关于
关于![]() 成轴对称,
成轴对称,
∴DF=DE,CF=CE,
∴DF=CF=CD,
∴△FDC为等边三角形;
(2)连接EF交DC于点G,
∵点![]() 、
、![]() 关于
关于![]() 成轴对称,
成轴对称,
∴FG=EG,CD⊥EF,
由(1)中可得DF=CF=4,
∴DG=CG=2,
∴FG=![]() ,
,
∴EF=![]() .
.

练习册系列答案
相关题目