题目内容
【题目】如图，直线y＝2x＋4与反比例函数y＝
的图象相交于A(－3，a)和B两点．
(1)求k的值；
(2)直线y＝m(m＞0)与直线AB相交于点M，与反比例函数的图象相交于点N.若MN＝4，求m的值；
(3)直接写出不等式
＞x的解集．
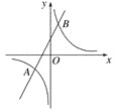
【答案】（1）6；（2）m=2或m=
；（3）x＜﹣1或5＜x＜6．
【解析】
试题（1）把点A（﹣3，a）代入y=2x+4与
即可得到结论；
（2）根据已知条件得到M（
，m），N（
，m），根据MN=4列方程即可得到结论；
（3）根据
得到
解不等式组即可得到结论．
试题解析：（1）∵点A（﹣3，a）在y=2x+4与的图象上，∴2×（﹣3）+4=a，∴a=﹣2，∴k=（﹣3）×（﹣2）=6；
（2）∵M在直线AB上，∴M（，m），N在反比例函数
上，∴N（，m），∴MN=xN﹣xm=﹣=4或xM﹣xN=
﹣=4，解得：∵m＞0，∴m=2或m=；
（3）由，得，∴
，∴
，∴
或
，得：
或
，∴此时x＜﹣1，由，得：
，∴5＜x＜6．
综上，原不等式的解集是：x＜﹣1或5＜x＜6．
练习册系列答案
名校课堂系列答案
相关题目
【题目】二次函数y=ax2+bx+c（a、b、c为常数且a≠0）中的x与y的部分对应值如下表：
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论：
（1）二次函数y=ax2+bx+c有最小值，最小值为﹣3；
（2）当﹣
＜x＜2时，y＜0；
（3）a﹣b+c=0；
（4）二次函数y=ax2+bx+c的图象与x轴有两个交点，且它们分别在y轴两侧
则其中正确结论的个数是（ ）
A. 1 B. 2 C. 3 D. 4
