Question

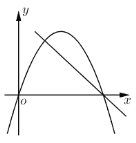
【题目】如图，圆心在坐标原点的⊙O，与坐标轴的交点分别为A、B和C、D．弦CM交OA于P，连结AM，已知tan∠PCO＝，PC、PM是方程x2﹣px+20＝0的两根．

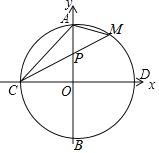
（1）求C点的坐标；

（2）写出直线CM的函数解析式；

（3）求△AMC的面积．

Answer 1

【答案】（1）点C坐标（﹣6，0）；（2）y＝x+4；（3）△AMC的面积为．

【解析】

（1）连接BC，根据一元二次方程根与系数的关系可求PCPM＝20，然后根据锐角三角函数设CO＝3x，PO＝2x，利用x表示出AP和BP，然后证出△AMP∽△CBP，列出比例式即可求出结论；

（2）设直线CM的函数解析式为：y＝kx+b，将点C、P的坐标代入即可求出结论；

（3）过点M作MN⊥AB于N，利用勾股定理求出PC即可求出PM，然后证出MN∥CO，即可证出△CPO∽△MPN，然后列出比例式即可求出MN，最后利用△AMC的面积＝×AP×（CO+MN）即可求出结论．

（1）如图，连接BC，

∵PC、PM是方程x2﹣px+20＝0的两根．

∴PCPM＝20，

∵tan∠PCO＝＝，

∴设CO＝3x，PO＝2x，

∵圆心在坐标原点的⊙O，与坐标轴的交点分别为A、B和C、D，

∴OC＝OB＝OD＝OA＝3x，

∴AP＝x，

∴BP＝5x，

∵∠AMC＝∠CBA，∠APM＝∠BPC，

∴△AMP∽△CBP，

∴，

∴PCPM＝APPB＝20，

∴x5x＝20，

∴x＝2，x＝-2（舍去）

∴CO＝6，OP＝4，

∴点C坐标（﹣6，0）；

（2）∵OP＝4，

∴点P（0，4）

设直线CM的函数解析式为：y＝kx+b，

∴

解得：

∴直线CM的函数解析式为：y＝x+4，

（3）如图，过点M作MN⊥AB于N，

∵CO＝6，OP＝4，

∴CP＝＝＝2，

∵CPPM＝20，

∴PM＝，

∵MN⊥AB，CO⊥AB，

∴MN∥CO，

∴△CPO∽△MPN，

∴，

∴＝

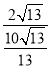∴MN＝，

∵△AMC的面积＝×AP×（CO+MN）＝×2×（6+）＝．