Question

【题目】如图，△ACB和△ECD都是等腰直角三角形，A、C、D三点在同一直线上，连接BD、AE，并延长AE交BD于F。

（1）求证：△ACE≌△BCD；

（2）直线AE与BD互相垂直吗?请证明你的结论。

Answer 1

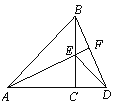
【答案】(1)、证明过程见解析；(2)、证明过程见解析.

【解析】

试题分析：(1)、根据等腰直角三角形的性质得出AC=BC，EC=CD，∠BCD=∠ACB=90°，从而得到三角形全等；(2)、直线AE与BD互相垂直就是证明∠AFD=90°，根据三角形全等得到∠AEC=∠BDC，结合∠BEF=∠AEC，从而得出∠BEF=∠BDC，根据DBC+∠BDC=90°得到∠BEF+∠DBC=90°，从而得到垂直.

试题解析：(1)、∵△ACB和△ECD都是等腰直角三角形，∴AC=BC EC=CD，

又∵∠BCD=∠ACB=90°，∴△ACE≌△BCD（SAS）

(2)、∵△ACE≌△BCD ∴∠AEC=∠BDC，又∵∠BEF=∠AEC（对顶角），

∴∠BEF=∠BDC，又∵∠DBC+∠BDC=90°，∴∠BEF+∠DBC=90°，∴AF⊥BD，所以直线AE与BD互相垂直。