题目内容
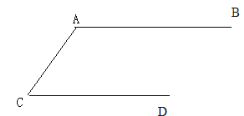
【题目】如图，AB∥CD.
（1）用直尺和圆规按要求作图：作∠ACD的平分线CP，CP交AB于点P；作AF⊥CP，垂足为F.
（2）判断直线AF与线段CP的关系，并说明理由.
【答案】（1）见解析；（2）直线AF是线段CP的垂直平分线，理由见解析.
【解析】
（1）根据尺规作图（作角平分线和过一点作已知直线的垂线）的方法，按要求作图即可；
（2）根据角平分线的定义和平行线的性质可得∠APC＝∠ACP，进而得到AP＝AC，然后根据线段垂直平分线的判定可得结论.
解：（1）CP，AF如图所示：
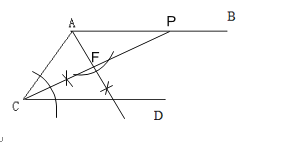
（2）直线AF是线段CP的垂直平分线，
理由：∵CP平分∠ACD，
∴∠ACP＝∠PCD，
∵AB∥CD，
∴∠APC＝∠PCD，
∴∠APC＝∠ACP，
∴AP＝AC，
又∵AF⊥CP，
∴直线AF是线段CP的垂直平分线.
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
