题目内容
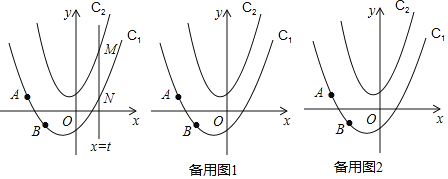
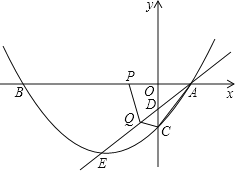
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C(0,﹣![]() ),OA=1,OB=4,直线l过点A,交y轴于点D,交抛物线于点E,且满足tan∠OAD=
),OA=1,OB=4,直线l过点A,交y轴于点D,交抛物线于点E,且满足tan∠OAD=![]() .
.
(1)求抛物线的解析式;
(2)动点P从点B出发,沿x轴正方形以每秒2个单位长度的速度向点A运动,动点Q从点A出发,沿射线AE以每秒1个单位长度的速度向点E运动,当点P运动到点A时,点Q也停止运动,设运动时间为t秒.
①在P、Q的运动过程中,是否存在某一时刻t,使得△ADC与△PQA相似,若存在,求出t的值;若不存在,请说明理由.
②在P、Q的运动过程中,是否存在某一时刻t,使得△APQ与△CAQ的面积之和最大?若存在,求出t的值;若不存在,请说明理由.
【答案】(1)抛物线的解析式为y=![]() ;(2)①存在t=
;(2)①存在t=![]() 或t=
或t=![]() ,使得△ADC与△PQA相似;②当t=
,使得△ADC与△PQA相似;②当t=![]() 时,△APQ与△CAQ的面积之和最大.
时,△APQ与△CAQ的面积之和最大.
【解析】(1)应用待定系数法求解析式
(2)①分别用t表示△ADC、△PQA各边,应用分类讨论相似三角形比例式,求t值;
②分别用t表示△APQ与△CAQ的面积之和,讨论最大值.
(1)∵OA=1,OB=4,
∴A(1,0),B(﹣4,0),
设抛物线的解析式为y=a(x+4)(x﹣1),
∵点C(0,﹣![]() )在抛物线上,
)在抛物线上,
∴﹣![]() ,
,
解得a=![]() .
.
∴抛物线的解析式为y=![]() .
.
(2)存在t,使得△ADC与△PQA相似.
理由:①在Rt△AOC中,OA=1,OC=![]() ,
,
则tan∠ACO=![]() ,
,
∵tan∠OAD=![]() ,
,
∴∠OAD=∠ACO,
∵直线l的解析式为y=![]() ,
,
∴D(0,﹣![]() ),
),
∵点C(0,﹣![]() ),
),
∴CD=![]() ,
,
由AC2=OC2+OA2,得AC=![]() ,
,
在△AQP中,AP=AB﹣PB=5﹣2t,AQ=t,
由∠PAQ=∠ACD,要使△ADC与△PQA相似,
只需![]() 或
或![]() ,
,
则有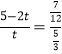 或
或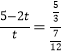 ,
,
解得t1=![]() ,t2=
,t2=![]() ,
,
∵t1<2.5,t2<2.5,
∴存在t=![]() 或t=
或t=![]() ,使得△ADC与△PQA相似;
,使得△ADC与△PQA相似;
②存在t,使得△APQ与△CAQ的面积之和最大,
理由:作PF⊥AQ于点F,CN⊥AQ于N,
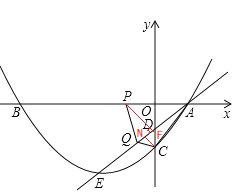
在△APF中,PF=APsin∠PAF=![]() ,
,
在△AOD中,由AD2=OD2+OA2,得AD=![]() ,
,
在△ADC中,由S△ADC=![]() ,
,
∴CN=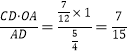 ,
,
∴S△AQP+S△AQC=![]() ,
,
∴当t=![]() 时,△APQ与△CAQ的面积之和最大.
时,△APQ与△CAQ的面积之和最大.