Question

【题目】已知：如图，在的内部，点、分别在射线、上，且,,，分别交、于点、.

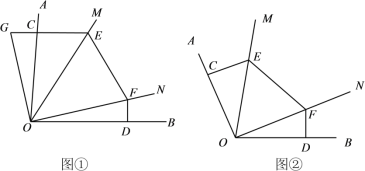
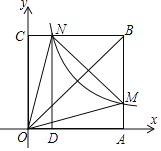
（1）如图①所示，若，，延长至点，使得，请证明EF=CE+DF；

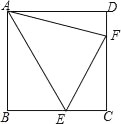
（2）如图②所示，若∠AOB=α，.求的度数.

Answer 1

【答案】（1）见解析；（2）∠MON＝.

【解析】

（1）易证△OCG≌△ODF（SAS），可得∠COG＝∠DOF，OG＝OF，再证明△EOG≌△EOF（SAS），得到EF＝EG，即证明EF＝CE＋DF；

（2）仿照（1）的思路，延长EC至G，使CG＝DF，连接OG，先证明△OCG≌△ODF（SAS），再证明△OEG≌△OEF（SSS），即可求得∠MON＝．

解：（1）∵CE⊥OA，DF⊥OB，

∴∠OCG＝∠ODF＝90°，

∵OC＝OD，CG＝DF，

∴△OCG≌△ODF（SAS），

∴∠COG＝∠DOF，OG＝OF，

∵∠AOB＝90°，∠MON＝45°，

∴∠COE＋∠DOF＝45°，

∴∠COE＋∠COG＝45°，即∠EOG＝45°＝∠MON，

在△EOG和△EOF中，，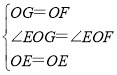

∴△EOG≌△EOF（SAS），

∴EF＝EG，

∴EF＝CE＋CG＝CE＋DF；

（2）如图②，延长EC至G，使CG＝DF，连接OG，

∵CE⊥OA，DF⊥OB，

∴∠OCG＝∠ODF＝90°，

∵OC＝OD，CG＝DF，

∴△OCG≌△ODF（SAS），

∴∠COG＝∠DOF，OG＝OF，

∵EG＝CE＋CG＝CE＋DF，EF＝CE＋DF，

∴EG＝EF，

∵OE＝OE，

∴△OEG≌△OEF（SSS），

∴∠EOG＝∠EOF，

∵∠EOG＋∠EOF＝∠COG＋∠AOF＝∠DOF＋∠AOF＝∠AOB＝α，

∴∠EOF＝∠AOB＝，即∠MON＝.