题目内容
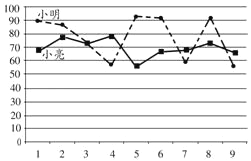
【题目】甲、乙两车间同时开始加工一批服装．从开始加工到加工完这批服装甲车间工作了9小时，乙车间在中途停工一段时间维修设备，然后按停工前的工作效率继续加工，直到与甲车间同时完成这批服装的加工任务为止．设甲、乙两车间各自加工服装的数量为y(件)．甲车间加工的时间为x(时)，y与x之间的函数图象如图所示，则下列结论错误的是( )
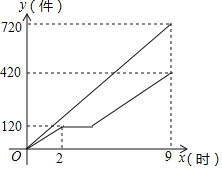
A.甲车间每小时加工服装80件
B.这批服装的总件数为1140件
C.乙车间每小时加工服装为60件
D.乙车间维修设备用了4小时
【答案】D
【解析】
根据图象确定两个车间的生产速度，再由乙车间剩余工作量推得复工后生产时间，得到乙车间加工零件数量y与x之间的函数关系式即可．
由图象可知，甲车间每小时加工零件个数为720÷9＝80个，则A正确；
由题意总零件个数为720+420＝1140个，则B正确；
乙车间生产速度为120÷2＝60个/时，则C正确；
乙车间复工后生产时间为(420﹣120)÷60＝5小时，故乙车间维修设备时间为9﹣5﹣2＝2小时，则D错误．
故选D．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某“兴趣小组”根据学习函数的经验，对函数y=x+
的图象和性质进行了探究，探究过程如下，请补充完整.
（1）函数y=x+
的自变量取值范围是________；
（2）下表是x与y的几组对应值：
x | … | -3 | -2 | -1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | - | -2 | - | - |
|
| 2 |
| m | … |
则表中m的值为________；
（3）根据表中数据，在如图所示平面直角坐标xOy中描点，并画出函数的一部分，请画出
（4）观察函数图象：写出该函数的一条性质
（5）进一步探究发现：函数y=x+图象与直线y=-2只有一交点，所以方程x+=-2只有1个实数根，若方程x+=k（x<0）有两个不相等的实数根，则k的取值范围是 ________.
