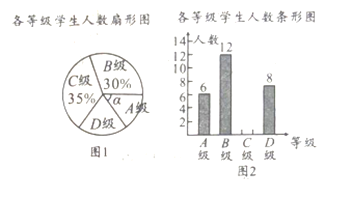
题目内容
【题目】如图，小明利用所学数学知识测量某建筑物BC高度，采用了如下的方法：小明从与某建筑物底端B在同一水平线上的A点出发，先沿斜坡AD行走260米至坡顶D处，再从D处沿水平方向继续前行若干米后至点E处，在E点测得该建筑物顶端C的仰角为72°，建筑物底端B的俯角为63°，其中点A、B、C、D、E在同一平面内，斜坡AD的坡度i=1：2.4，根据小明的测量数据，计算得出建筑物BC的高度约为（ ）米（计算结果精DE确到0.1米，参考数据：sin72°≈0.95，tan72°≈3.08，sin63°≈0.89，tan63°≈1.96）
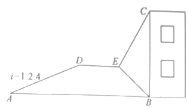
A.157.1 B.157.4 C.257.4 D.257.1
【答案】D
【解析】
如图作DH⊥AB于H，延长DE交BC于F．则四边形DHBF是矩形，在Rt△ADH中求出DH，再在Rt△EFB中求出EF，在Rt△EFC中求出CF即可解决问题
如图作DH⊥AB于H，延长DE交BC于F．
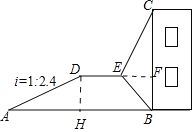
在Rt△ADH中，∵AD=260，DH：AH=1：2.4，
∴DH=100（m），
∵四边形DHBF是矩形，
∴BF=DH=100，
在Rt△EFB中，tan63°=
，
∴EF=
，
在Rt△EFC中，FC=EFtan72°，
∴CF=
×3.08≈157.1，
∴BC=BF+CF=257.1（m）．
故选D．
【题目】九年级某数学小组在学完《直角三角形的边角关系》这章后，决定用所学的知识设计遮阳篷（要求：遮阳篷既能最大限度地遮挡夏天炎热的阳光，又能最大限度地使冬天温暖的阳光射入室内）．他们制定了设计方案，并利用课余时间完成了调查和实地测量．调查和测量项目及结果如下表：
项目 | 内容 | |
课题 | 设计遮阳篷 | |
测量示意图 |
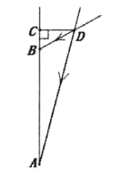
| 如图，设计了垂直于墙面AC的遮阳篷CD，AB表示窗户的高度．榆次区一年中，夏至这一天的正午时刻，太阳光线DA与遮阳篷CD的夹角∠ADC最大；冬至这一天的正午时刻，太阳光线DB与遮阳篷CD的夹角∠CDB最小． |
调查数据 |
|
|
测量数据 |
| |
… | … | |
根据上述方案及数据，求遮阳篷
的长．
（结果精确到
，参考数据：
，
，
，
，
，
）