Question

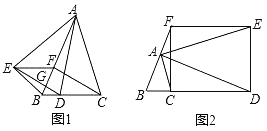
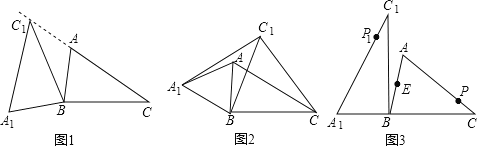
【题目】在锐角△ABC中，AB＝6，BC＝11，∠ACB＝30°，将△ABC绕点B按逆时针方向旋转，得到△A1BC1．

(1)如图1，当点C1在线段CA上时，∠CC1A1＝_____°；

(2)如图2，连接AA1，CC1．若△ABA1的面积为24，求△CBC1的面积；

(3)如图3，点E为线段AB中点，点P是线段AC上的动点，在△ABC绕点B按逆时针方向旋转过程中，点P的对应点是P1，求在旋转过程中，线段EP1长度的最大值与最小值的差．

Answer 1

【答案】(1)60；(2)＝；(3)11.5．

【解析】

(1)根据旋转的性质可知：∠A1C1B＝30°，再由等边对等角得∠BC1C＝30°，则∠CC1A1＝60°；

(2)由△ABC≌△A1BC1得比例式，证明△ABA1∽△CBC1，根据面积比等于相似比的平方求出△CBC1的面积；

(3)作辅助线，当点P在D处时BP最小，则BP1最小，EP1最小；当点P在点C处时，BP最大，则BP1最大，EP1最大，代入计算．

(1)如图1，

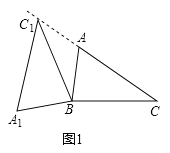
由旋转得：∠A1C1B＝∠C＝30°，BC＝BC1，

∴∠C＝∠BC1C＝30°，

∴∠CC1A1＝60°，

故答案为：60；

(2)如图2，

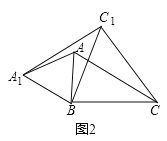
∵△ABC≌△A1BC1，

∴BA＝BA1，BC＝BC1，∠ABC＝∠A1BC1，

∴，

∵∠ABA1＝∠CBC1，

∴△ABA1∽△CBC1，

∴＝，

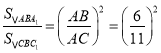∵＝24，

∴＝；

(3)如图4，过点B作BD⊥AC，D为垂足，

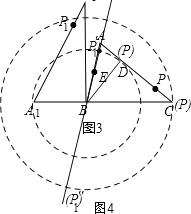
∵△ABC为锐角三角形，

∴点D在线段AC上，

在Rt△BCD中，BD＝BC×sin30°＝5.5，

以B为圆心，BD为半径画圆交AB于P1′，BP1有最小值BP1′．

∴EP1的最小值为5.5﹣3＝2.5，

以B为圆心，BC为半径画圆交AB的延长线于P1″，BP1有最大值BP1″．

此时EP1的最大值为11+3＝14，

∴线段EP1的最大值与最小值的差为14﹣2.5＝11.5．