题目内容
【题目】某“兴趣小组”根据学习函数的经验，对函数y=x+
的图象和性质进行了探究，探究过程如下，请补充完整.
（1）函数y=x+
的自变量取值范围是________；
（2）下表是x与y的几组对应值：
x | … | -3 | -2 | -1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | - | -2 | - | - |
|
| 2 |
| m | … |
则表中m的值为________；
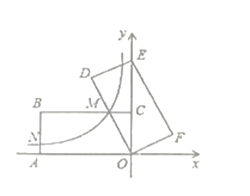
（3）根据表中数据，在如图所示平面直角坐标xOy中描点，并画出函数的一部分，请画出
（4）观察函数图象：写出该函数的一条性质
（5）进一步探究发现：函数y=x+图象与直线y=-2只有一交点，所以方程x+=-2只有1个实数根，若方程x+=k（x<0）有两个不相等的实数根，则k的取值范围是 ________.
【答案】（1）x≠0；（2）m=
；（3）见解析；（4）见解析；（5）k＜-2.
【解析】
（1）根据分式有意义的条件是分母不等于零列出不等式，从而求出自变量x的取值范围；
（2）根据表中数据的规律可得m的值；
（3）根据表中数据，先描点，再连线即可得这部分的函数图象；
（4）观察表中数据和函数图象的特征，写出其中一条性质即可.
（5）从图象上可以看出，当x<0时，在直线y=-2的下方，函数y=x+
图象与直线y=k有两个交点，即方程x+=k（x<0）有两个不相等的实数根，故可得k的取值范围.
（1）根据分式有意义的条件是分母不等于零得，x≠0
（2）当x=3时，y=x+=
．
∴m=
（3）如图：
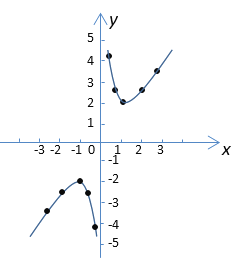
（4）(答案不唯一)该函数无最大值，也无最小值；函数图象关于原点对称；当x＜-1时， y随x增大而增大；
（5）∵x+
=k(x<0)有两个不相等的实数根，
∴k＜-2．
故答案为：k＜-2.
应用题作业本系列答案
【题目】红树林学校在七年级新生中举行了全员参加的“防溺水”安全知识竞赛，试卷题目共10题，每题10分．现分别从三个班中各随机取10名同学的成绩（单位：分），收集数据如下：
1班：90，70，80，80，80，80，80，90，80，100；
2班：70，80，80，80，60，90，90，90，100，90；
3班：90，60，70，80，80，80，80，90，100，100．
整理数据：
分数 人数 班级 | 60 | 70 | 80 | 90 | 100 |
1班 | 0 | 1 | 6 | 2 | 1 |
2班 | 1 | 1 | 3 |
| 1 |
3班 | 1 | 1 | 4 | 2 | 2 |
分析数据：
平均数 | 中位数 | 众数 | |
1班 | 83 | 80 | 80 |
2班 | 83 |
|
|
3班 |
| 80 | 80 |
根据以上信息回答下列问题：
（1）请直接写出表格中
的值；
（2）比较这三组样本数据的平均数、中位数和众数，你认为哪个班的成绩比较好？请说明理由；
（3）为了让学生重视安全知识的学习，学校将给竞赛成绩满分的同学颁发奖状，该校七年级新生共570人，试估计需要准备多少张奖状？
